1、问题描述
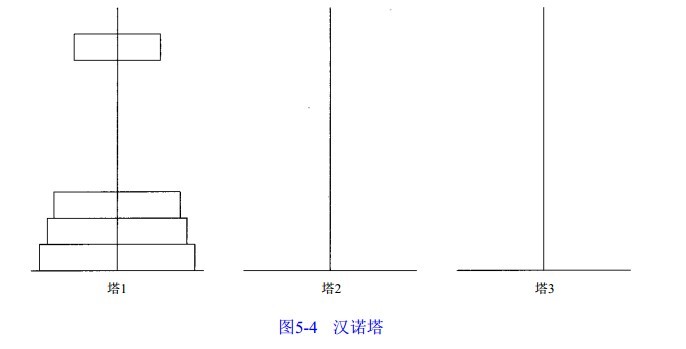
汉诺塔( Towers of Hanoi)问题来自一个古老的传说:在世界刚被创建的时候有一座钻石宝塔(塔1 ),其上有6 4个金碟(如图 5 - 4所示)。所有碟子按从大到小的次序从塔底堆放至塔顶。紧挨着这座塔有另外两个钻石宝塔(塔 2和塔3)。从世界创始之日起,婆罗门的牧师们就一直在试图把塔 1 上的碟子移动到塔 2上去,其间借助于塔 3的帮助。由于碟子非常重,因此,每次只能移动一个碟子。另外,任何时候都不能把一个碟子放在比它小的碟子上面。按照这个传说,当牧师们完成他们的任务之后,世界末日也就到了。在汉诺塔问题中,已知 n个碟子和 3 座塔。初始时所有的碟子按从大到小次序从塔 1 的底部堆放至顶部,我们需要把碟子都移动到塔 2,每次移动一个碟子,而且任何时候都不能把大碟子放到小碟子的上面。在继续往下阅读之前,可以先尝试对 n= 2 , 3和4来解决这个问题。
一个非常优雅的解决办法是使用递归。为了把最大的碟子移动到塔 2,必须把其余n- 1 个碟子移动到塔 3,然后把最大的碟子移动到塔 2。接下来是把塔 3上的 n- 1 个碟子移动到塔 2,为此可以利用塔 2和塔1 。可以完全忽视塔 2上已经有一个碟子的事实,因为这个碟子比塔 3上将要移过来的任一个碟子都大,因此,可以在它上面堆放任何碟子。事实上递归本身就是用堆栈实现的。
盘子移动次数为:
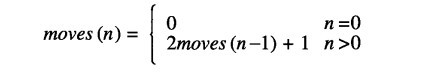
推导可得moves(n)=2n-1,可以证明这实际上是最少移动次数
假定希望给出每次移动之后三座塔的状态(即塔上的碟子及其次序),那么必须在内存中保留塔的状态,并在每次移动碟子之后,对塔的状态进行修改。这样每移动一个碟子时,就可以在一个输出设备(如计算机屏幕、打印机等)上输出塔的信息。由于从每个塔上移走碟子时是按照 L I F O的方式进行的,因此可以把每个塔表示成一个堆栈。三座塔在任何时候都总共拥有 n 个碟子,因此,如果使用链表形式的堆栈,只需申请 n个元素所需要的空间。如果使用的是基于公式化描述的堆栈,塔 1和塔2的容量都必须是 n,而塔3的容量必须为 n- 1 ,因而所需要的空间总数为 3n- 1 。前面的分析已经指出,汉诺塔问题的复杂性是以 n 为指数的函数,因此在可以接受的时间范围内,只能解决 n 值比较小(如 n≤ 3 0)的汉诺塔问题。对于这些较小的 n 值,基于公式描述和基于链表描述的堆栈在空间需求上的差别相当小,因此可以随意使用。
本文使用基于链表描述的堆栈实现。
2、代码实现
汉诺塔程序(其中LinkedStack.h实现见堆栈的链表方式实现):
1 #ifndef HANOICLASS_H 2 #define HANOICLASS_H 3 #include <iostream> 4 #include "LinkedStack.h" 5 6 using std::cout; 7 using std::endl; 8 9 class Hanoiclass 10 { 11 friend void TowersOfHanoi(int); 12 public: 13 void TowersOfHanoi(int n, int x, int y, int z);//递归解决汉诺塔 14 private: 15 LinkedStack<int> *S[4]; 16 void ShowState();//输出3个塔的状态 17 }; 18 19 void Hanoiclass::TowersOfHanoi(int n, int x, int y, int z) 20 { 21 if (n > 0) 22 { 23 TowersOfHanoi(n - 1, x, z, y); 24 cout << "Move top disk from tower " << x << "to top of tower " << y << std::endl; 25 int temp; 26 S[x]->Delete(temp);//从x塔顶移出盘子 27 S[y]->Add(temp);//盘子移入y塔顶 28 ShowState(); 29 TowersOfHanoi(n - 1, z, y, x); 30 } 31 } 32 33 void TowersOfHanoi(int n) 34 { 35 Hanoiclass X; 36 for (int i = 1; i < 4;++i) 37 { 38 X.S[i] = new LinkedStack<int>; 39 } 40 41 for (int d = n; d>0;--d) 42 { 43 X.S[1]->Add(d); 44 } 45 X.ShowState(); 46 X.TowersOfHanoi(n, 1, 2, 3); 47 48 } 49 50 void Hanoiclass::ShowState() 51 { 52 for (int i = 1; i < 4;++i) 53 { 54 cout << "塔"<<i<<": "; 55 if (!S[i]->IsEmpty()) 56 { 57 cout << *S[i]; 58 } 59 cout << endl; 60 } 61 62 } 63 #endif
运行:
1 // Hanoi.cpp : 定义控制台应用程序的入口点。 2 // 3 4 #include "stdafx.h" 5 #include<iostream> 6 #include "Hanoiclass.h" 7 using std::cout; 8 using std::cin; 9 10 int _tmain(int argc, _TCHAR* argv[]) 11 { 12 TowersOfHanoi(3); 13 system("pause"); 14 return 0; 15 }
输出:
