[Luogu1938][USACO09NOV]找工就业Job Hunt

原题链接：https://www.luogu.org/problem/show?pid=1938

这一道题有一个比较难的点就是，这一张图上，是点上有权。既然点上有权的话，我们就不好一下子使用最短路了。
我们想一下，我们从A走向B就一定是会在A与B处赚多钱是不是。这样的话，我们就不妨将点权转化到指向它的边上。
然后，对于本身带权的边，就用点权减去边原来带的权。
这样，我们以起点开始，起点的点权为起点的dist的值（这个很好理解的吧），跑一边最长路即可。这里我们需要判一下正环，就跟在最短路中SPFA判负环一样，如果一个点入队超过n次，就说明存在负环（本题的正环）

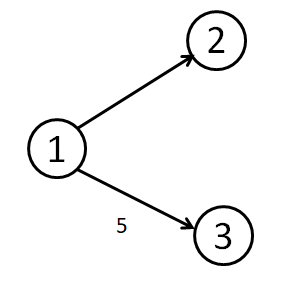
在这张图中，所有点的权为4。所以，我们可以把这张图转化一下。

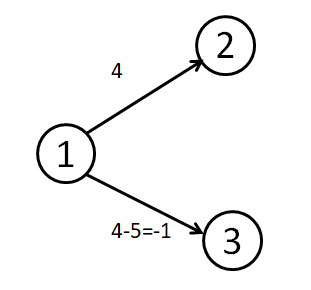
在我们这一张新图中，我们像刚刚说的那样，以起点的权为起点dist初值，跑最长路即可。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
#define rep(i,a,n) for(register int i=(a);i<=(n);++i)
#define per(i,a,n) for(register int i=(a);i>=(n);--i)
#define fec(i,x) for(register int i=head[x];i;i=Next[i])
#define debug(x) printf("debug:%s=%d
",#x,x)
#define mem(a,x) memset(a,x,sizeof(a))
template<typename A>inline void read(A&a){a=0;A f=1;int c=0;while(c<'0'||c>'9'){c=getchar();if(c=='-')f*=-1;}while(c>='0'&&c<='9'){a=a*10+c-'0';c=getchar();}a*=f;}
template<typename A,typename B>inline void read(A&a,B&b){read(a);read(b);}
template<typename A,typename B,typename C>inline void read(A&a,B&b,C&c){read(a);read(b);read(c);}

const int maxn=220+7,maxm=500+7;
int u[maxm],v[maxm],w[maxm],Next[maxm],head[maxn],tot;
int d,p,n,f,s,ans,x,y,z;
int dist[maxn],cnt[maxn];
bool inq[maxn];
queue<int>q;
inline void addedge(int x,int y,int z){
	u[++tot]=x;v[tot]=y;w[tot]=z;
	Next[tot]=head[x];head[x]=tot;
}

bool SPFA(int s){
	mem(dist,-0x7f);inq[s]=1;q.push(s);dist[s]=d;
	while(!q.empty()){
		int x=q.front();q.pop();inq[x]=0;
		fec(i,x)
			if(dist[v[i]]<dist[x]+w[i]){
				dist[v[i]]=dist[x]+w[i];
				if(!inq[v[i]]){
					inq[v[i]]=1;q.push(v[i]);++cnt[v[i]];
					if(cnt[v[i]]>n)return 0;
				}
			}
	}
	return 1;
}

void Init(){
	read(d,p);read(n,f,s);
	rep(i,1,p){
		read(x,y);
		addedge(x,y,d);
	}
	rep(i,1,f){
		read(x,y,z);
		addedge(x,y,d-z);
	}
}

void Work(){
	int ans=SPFA(s);
	if(!ans)printf("-1
");
	else{
		ans=-0x7f7f7f7f;
		rep(i,1,n)ans=max(ans,dist[i]);
		printf("%d
",ans);
	}
}

int main(){
	Init();
	Work();
	return 0;
}