监控二叉树

题目来源：https://leetcode-cn.com/problems/binary-tree-cameras/

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

 

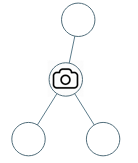
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。
示例 2：

 

输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。

题解：暴力超时：遍历各个节点，每个节点两种情况，亮灯或者不亮灯（代表相机），是否亮灯影响下面节点，所以加一个遍历参数间隔，间隔最大可以为2，当为2时必然要亮灯，当深度为1时两个孩子亮1个即可，取各情况的最小值即为最优解。但是节点数量最大为1000，暴力时间复杂度log(2*2)n，肯定超时，应该是动态规划解，后面补充正确解法。

public class 监控二叉树968 {

    public int minCameraCover(TreeNode root, int interval) {

        if(root == null){
            return 0;
        }
        if(interval == 1 && root.left == null && root.right == null){
            //当没有孩子节点，父节点也没有照到，则亮灯
            root.val = 1;
            return 1;
        }

        if(interval == 1 && root.left != null && root.right != null){
            // 当有1个间隔，两个孩子，两个孩子中的一个能照到此节点就好
            root.val = 1;
            int x = minCameraCover(root.left, 0) + minCameraCover(root.right, 0) + 1;
            root.val = 0;
            int y = minCameraCover(root.left, interval) + minCameraCover(root.right, interval + 1);
            int z = minCameraCover(root.left, interval + 1) + minCameraCover(root.right, interval);
            // 此节点可亮可不亮，三种情况对比，选择最优解
            if(x < Math.min(y, z)){
                root.val = 1;
                return x;
            } else {
                return Math.min(y, z);
            }
        }

        if(interval == 2){
            //深度为2，一点要亮灯
            root.val = 1;
            return minCameraCover(root.left, 0) + minCameraCover(root.right, 0) + 1;
        }else {
            // 深度为1，此节点可亮可不亮
            root.val = 1;
            int x = minCameraCover(root.left, 0) + minCameraCover(root.right, 0) + 1;
            root.val = 0;
            int y = minCameraCover(root.left, interval + 1) + minCameraCover(root.right, interval + 1);
            if(x < y){
                // 找到最小的情况
                root.val = 1;
                return x;
            } else {
                return y;
            }

        }
    }


    public int minCameraCover(TreeNode root){
        return minCameraCover(root, 1);
    }

    private static TreeNode buildTree(){
        int nextInt = Input.cin.nextInt();
        if(nextInt == 0){
            TreeNode treeNode = new TreeNode(0);
            treeNode.left = buildTree();
            treeNode.right = buildTree();
            return treeNode;
        }
        return null;
    }
    public static void main(String[] args) {
        TreeNode treeNode = buildTree();
        int x = new 监控二叉树968().minCameraCover(treeNode);
        System.out.println(x);
    }
}

正确解法：

前面的暴力明显反应了父亲，当前节点，和孩子的关系，那么可以将这些关系总结为3个状态，1. 当前节点有相机，2. 当前节点放不放都行（全局最优），3. 两个子树都被覆盖

然后遍历，在每个阶段都求最优解：

第1个状态：左右子树的第三个状态之和 + 当前节点的相机

第3个状态：左右子树的全局最优和

第2个状态： 左树有相机+右树最优  或   左树最优+右树有相机

得到最终代码：

public class 监控二叉树968 {


    public int[] trave(TreeNode root){
        if(root == null){
            //当前root有相机, 当前root放或者不放摄像头都行，两个子树被覆盖（不管root）
            return new int[]{Integer.MAX_VALUE / 2, 0, 0};
        }
        int[] left = trave(root.left);
        int[] right = trave(root.right);
        int[] array = new int[3];
        //两个孩子都被他们的孩子监控的最优解 + 1（有相机）
        array[0] = left[2] + right[2] + 1;
        // 左孩子有相机 或者右孩子有相机时分别加上另外一个孩子的最优解
        array[1] = Math.min(array[0], Math.min(left[0] + right[1], left[1] + right[0]));
        //不管当前节点，取孩子们的最优解
        array[2] = Math.min(array[0], left[1] + right[1]);
        return array;
    }
    public int minCameraCover(TreeNode root){
        int[] trave = trave(root);
        return trave[1];
    }

    private static TreeNode buildTree(){
        int nextInt = Input.cin.nextInt();
        if(nextInt == 0){
            TreeNode treeNode = new TreeNode(0);
            treeNode.left = buildTree();
            treeNode.right = buildTree();
            return treeNode;
        }
        return null;
    }
    public static void main(String[] args) {
        TreeNode treeNode = buildTree();
        int x = new 监控二叉树968().minCameraCover(treeNode);
        System.out.println(x);
    }
}

转载请注明地址：http://www.cnblogs.com/handsomecui/