题目

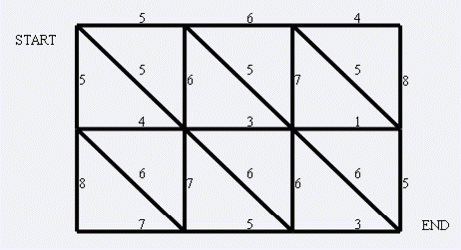
现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的, 而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个网格的地形: 左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 1:(x,y)<==>(x+1,y) 2:(x,y)<==>(x,y+1) 3:(x,y)<==>(x+1,y+1) 道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的. 左上角和右下角为兔子的两个窝, 开始时所有的兔子都聚集在左上角(1,1)的窝里,现在它们要跑到右下解(N,M)的窝中去,狼王开始伏击 这些兔子.当然为了保险起见,如果一条道路上最多通过的兔子数为K,狼王需要安排同样数量的K只狼, 才能完全封锁这条道路,你需要帮助狼王安排一个伏击方案,使得在将兔子一网打尽的前提下,参与的 狼的数量要最小。因为狼还要去找喜羊羊麻烦. Input 第一行为N,M.表示网格的大小,N,M均小于等于1000. 接下来分三部分 第一部分共N行,每行M-1个数,表示横向道路的权值. 第二部分共N-1行,每行M个数,表示纵向道路的权值. 第三部分共N-1行,每行M-1个数,表示斜向道路的权值. 输入文件保证不超过10M Output 输出一个整数,表示参与伏击的狼的最小数量. Sample Input 3 4 5 6 4 4 3 1 7 5 3 5 6 7 8 8 7 6 5 5 5 5 6 6 6 Sample Output 14
题目图片
讲这部分之前,请先阅读以上的文章(讲得十分好%%%)(当然阅读到27页就好了)
读完后,我们发现这道题完全可以用其对偶图来跑最短路。
原图 对偶图
面数 x 面数 y
点数 y 那么其对偶图中 点数 x
边数 z 边数 z
面数和点数正好相反。
将原图的起点和终点连接起来,建立一个新的面(这是必须的)。
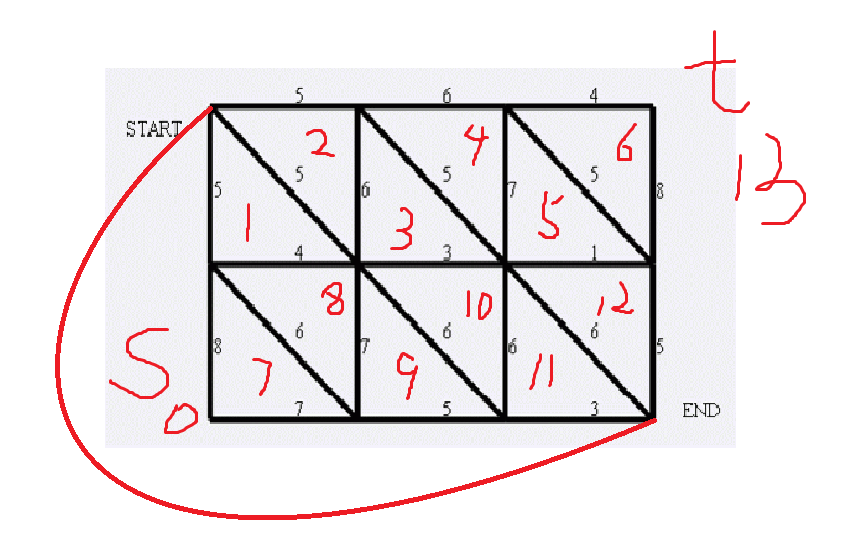
当然s点和t点之间是没有边的。
s和1,7,9,11之间有边。
t和2,4,6,12之间有边。
上面是我们建好的对偶图,从左至右依次编号,关于对偶图中面的编号,因为我们是按照横边,纵边,斜边的顺序读入的,所以我们一定要按照一定的方法对这些图编号
我采用的是从左至右依次编号,因为我们可以很清楚当前边连接的两个点(原图中的两个面)所在的位置,因为这是平面图,所以可以用欧拉公式来求出之前有多少点(
原图中的面)。再加上这个点(原图中的面(重要的事说三遍))在当前行中的位置就是它的编号。
只要原图中的两个面之间存在边,那么它的对偶图中的两个点就存在边。
#include<stdio.h> #include<string.h> #include<algorithm> using namespace std; int cnt, i, j, x, xx, xxx, h, t, s, hh[2010000], n, m, w; bool dd[2010000]; int e, l[2010000], d[1010000], hhh, ww; struct node { int v, next, z; } b[6010000]; inline void add(int aa, int bb, int cc)//邻接表,建双向边 { b[++cnt].v = bb; b[cnt].next = hh[aa]; b[cnt].z = cc; hh[aa] = cnt; b[++cnt].v = aa; b[cnt].next = hh[bb]; b[cnt].z = cc; hh[bb] = cnt; } void add1() { for(i = 1; i < m; ++i) { scanf("%d", &x); add(i * 2, t, x); } for(i = 2; i < n; ++i) { for(j = 1; j < m; ++j) { scanf("%d", &x); add((i - 1) * (m - 1) * 2 + j * 2, (i - 1) * (m - 1) * 2 + j * 2 - m * 2 + 1, x);//利用欧拉公式确定编号并建边(下面的add函数也是如此) } } for(j = 1; j < m; ++j) { scanf("%d", &x); add(s, (n - 2) * 2 * (m - 1) + j * 2 - 1, x); } } void add2() { for(i = 1; i < n; ++i) { scanf("%d", &x); xx = (i - 1) * (m - 1) * 2 + 1; add(s, xx, x); for(j = 2; j < m; ++j) { scanf("%d", &x); xx += 2; add(xx - 1, xx, x); } scanf("%d", &x); add(xx + 1, t, x); } } inline void add3() { for(i = 1; i < n; ++i) { for(j = 1; j < m; ++j) { scanf("%d", &x); add((i - 1) * (m - 1) * 2 + j * 2, (i - 1) * (m - 1) * 2 + j * 2 - 1, x); } } }
//下面的spfa中一定要用循环队列,省空间。不用的话空间开小(这很有可能毕竟1百万个点)可能会被卡。 void spfa() { dd[s] = true; h = 0; w = 0; memset(l,0x3f,sizeof(l));//将l数组赋成最大值
//hhh记录的是我们用的是队列中第几个元素(实际上)
//ww记录的是队列中总共有几个元素 l[s] = 0; while(1) { if(hhh > ww)break; h = hhh % 1000001; w = ww % 1000001; for(i = hh[s]; i; i = b[i].next) { e = b[i].v; if(l[s] + b[i].z < l[e]) { l[e] = l[s] + b[i].z; if(!dd[e])w = ww % 1000000, d[++w] = e, ww++, dd[e] = true; } } dd[s] = false; h = hhh % 1000000; s = d[++h]; hhh++; } } int main() { scanf("%d %d", &n, &m); if(n == m && n == 1)//特判 { printf("0"); return 0; } s = 0; t = 2 * (n - 1) * (m - 1) + 1; add1();//读入横边 add2();//读入纵边 add3();//读入斜边 spfa();//对其对偶图求s————t的最短路 printf("%d", l[t]); return 0; }
