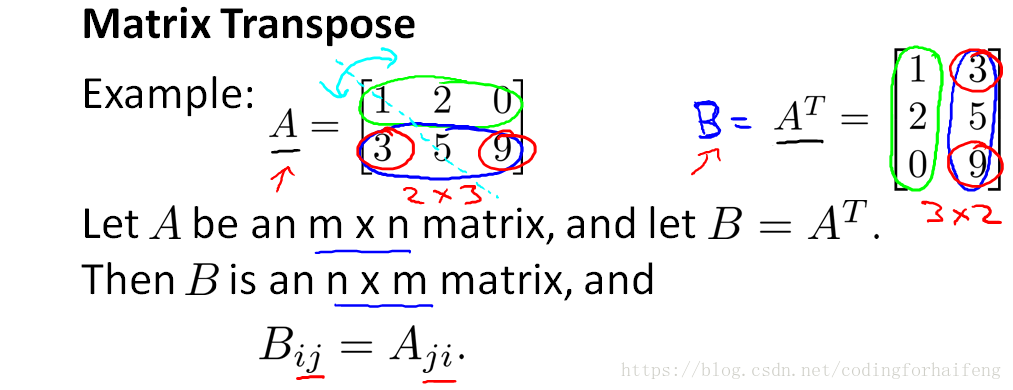矩阵(matrices)和向量(vectors)
矩阵(matrix)
定义:由数字组成的矩形阵列(Rectangular array of numbers)。矩阵其实是二维数组的另一种说法。
矩阵的维数(Dimension of matrix):矩阵的行数X矩阵的列数
矩阵的项(entries of matrix):如果A是个矩阵,Aij表示的是第i行第j列所对应的元素
向量(vector)
定义:向量是一种特殊的矩阵,向量是只有一列的矩阵
向量的维数:nx1矩阵,叫做n维向量
向量的项:如果B是一个向量,则Bi表示向量B的第i个元素,下标从1开始
一般用大写字母如A、B、C表示矩阵,小写字母如y表示向量
加法和标量乘法
矩阵的加法:
两个矩阵对应位置的元素进行相加,注意,只有相同维度的两个矩阵才可以相加,结果为与相加的两个矩阵相同维数的矩阵。不同维数的两个矩阵相加是没有意义的,或者说是错误的。
矩阵的减法亦同理,只是加上的是相反数。
矩阵与标量的乘法运算:
矩阵与标量进行乘法运算时,分别拿标量与矩阵中的每一项进行相乘,结果作为对应的项的元素,注意,这里的标量指的是实数。
矩阵与标量相除,其实就是矩阵与标量的倒数相乘。
矩阵向量的乘法
矩阵与向量相乘:
m*n x n*1 = m*1即矩阵的列数要与向量的行数相同,结果为一个行数等于矩阵行数,列数等于向量列数的向量。具体的实现过程请看下图:
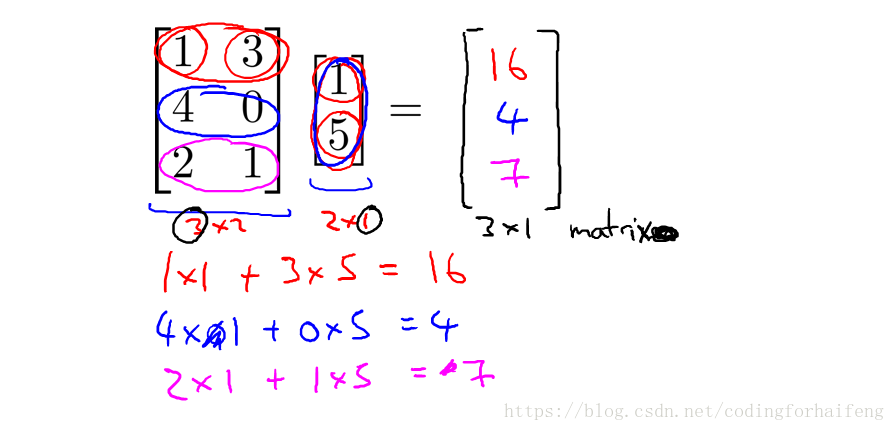
矩阵乘法
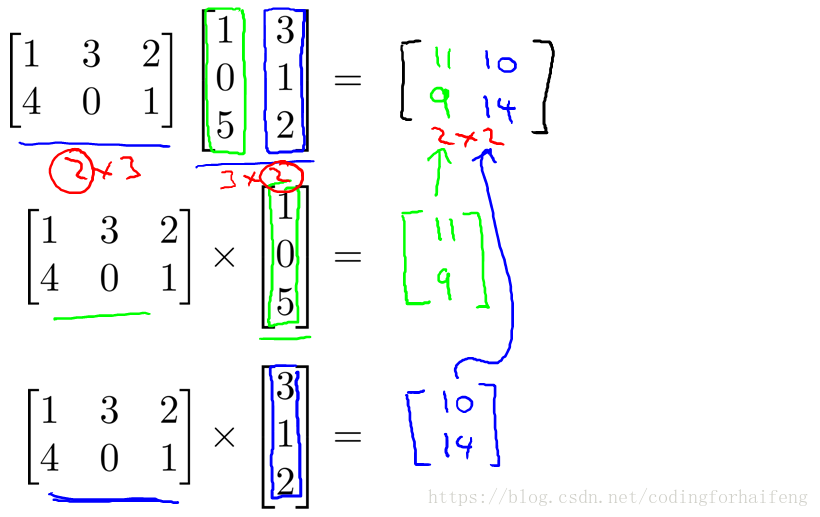
矩阵与矩阵相乘:
m*n x n*o = m*o即矩阵的列数要与向量的行数相同,结果为一个行数等于矩阵行数,列数等于向量列数的向量。其步凑为用左边的矩阵与中间矩阵的第一列相乘,得到右边矩阵的第一列,以此类推(联想矩阵与向量相乘)。具体的实现过程如下:
矩阵的乘法特征
交换律
通常情况下,矩阵的乘法运算是不符合交换律的,即AxB !=(不等于) BxA。如Amxn x Bnxm = Cmxm,而Bnxm x Amxn = Dnxn。显然,n与m并不一定相等。也就是说,交换之后会改变维度。特殊情况,单位矩阵时是可以成立的。
结合律
事实证明,矩阵的乘法运算是符合结合律,即AxBxC = Ax(BxC)。
单位矩阵
它是一个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1,其余以外全部为0。任何矩阵与单位矩阵相乘都等于其本身。
矩阵的逆运算和转置运算
矩阵逆运算(Matrix inverse):
如果A是一个mxm的矩阵(方阵,矩阵的行数与列数相同),假设A矩阵具有逆矩阵(只有是mxm的矩阵才具有逆矩阵,即只有方阵才有逆矩阵)
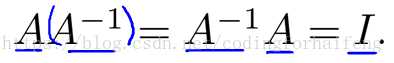
不存在逆矩阵的矩阵,如所有项元素都为0的矩阵,我们称之为奇异矩阵或者退化矩阵
矩阵的转置矩阵(transpose):
假设A是一个mxn的矩阵,并设矩阵B等于A的转置,那么B是一个nxm的矩阵