Machine Learning的定义
AI发展出来的一个领域,计算机开发的一项新功能
定义一:
在没有明确设置的情况下,使计算机具有学习能力的研究领域。 ——Samuel(1959)
定义二:
一个适当的学习问题定义如下:计算机程序从经验E中学习解决某一任务T进行某一性能度量P,通过P测定在T上的表现因经验E而提高。 ——Tom Mitchell(1998)
Machine Learning的应用领域
1.数据挖掘(Database mining)
——Web click data,medical records,biology,engineering
2.无法手动编写的程序(Applications can't program by hand)
——自然语言处理(NLP),计算机视觉(Computer Vision),手写识别(handwriting recognition),自动化(Autonomous)
3.个性化推荐(self-customizing programs)
——商品推荐
4.AI:像人类一样学习(Understanding human learning(brain,real AI))
Machine Learning算法分类
1.监督学习(Supervised learning)
2.无监督学习(Unsupervised learning)
3.强化学习(Reinforcement learning)
4.推荐系统(recommender systems)
机器学习算法之——监督学习(Supervised learning)
定义:监督学习是指我们给算法一个数据集,其中包含了“正确答案”,算法的目的是给出更多正确的答案。即根据数据进行结果预测,分为回归(Regression)问题和分类(Classification)问题
回归(Regression):预测一个连续值的输出(即具体的数值)
分类(Classification):预测一个离散值的输出(0 or 1),分类的结果可能有多种(1,2,3,4,and so on)
机器学习算法之——无监督学习(Unsupervised learning)
定义:无监督学习(聚类算法),将所给的数据进行分簇,事先并没有给出分簇的规则,即没有给出“正确的答案”,这里不同于监督学习。(告诉计算机,这是一堆数据,我不知道这些数据是什么,不知道是什么类型以及有哪些类型的数据,你能自动找出这些数据的结构吗?你能自动按得到的类型把这些数据分成簇吗?)
应用:大型计算机集群、社交网络分析、市场分析、天文数据分析
聚类只是无监督学习中的一种,比如还有,鸡尾酒会问题算法
机器学习例子之——房价预测
模型(model):
m——表示训练样本的数量(Number of training examples)
x——表示输入变量(‘input’variable or features)
y——表示输出变量(‘output’variable or features)
(x,y)——表示一个训练样本(one training example)
单变量线性回归(Univariate linear regression)
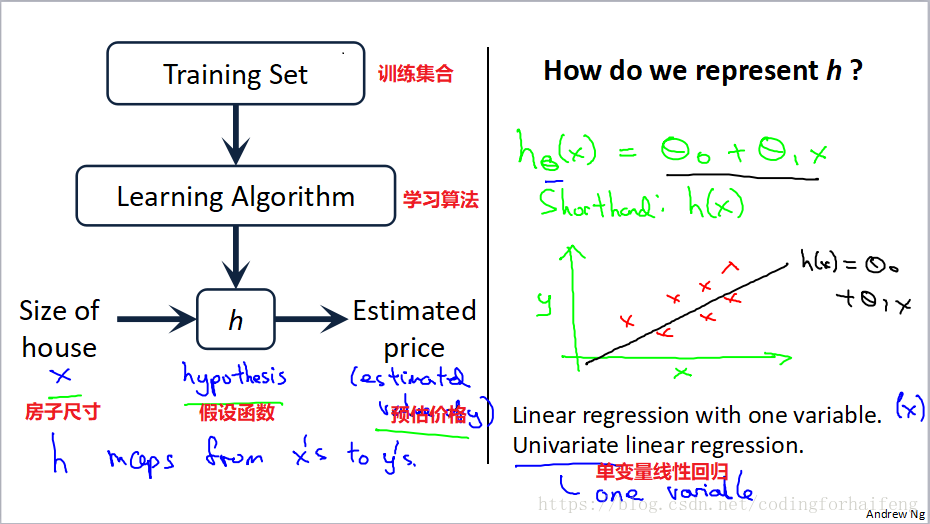
假设函数(Hpothesis):
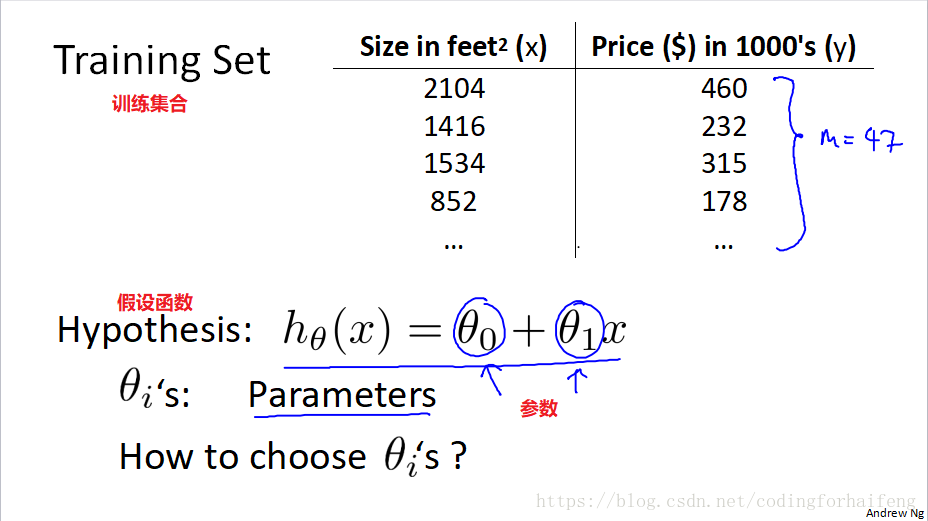
代价函数(Cost Function):
——其意义在于找到假设函数的最佳参数,从而确定最佳的假设函数。代价函数又称为平方误差函数,或者平方误差代价函数,这是解决线性回归问题常用的函数。这里需要用到均方误差(square error cost function),所以,需要回去好好复习均方误差。

均方误差(square error cost function):
定义:表示参数预估值与参数真值之差平方的期望值,记为MSE。机器学习中它经常被用于表示预测值和实际值相差的程度。
数学表达式:
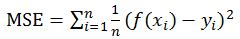
梯度下降(Gradient descent):
定义:梯度下降是迭代法中的一种,可以用于求解最小二乘问题。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。(百度百科)

等高线图:将三维的空间图转化为二维图形求两个参数下的代价函数最小值。不同的梯度下降起始点可能会得到不同的局部最优点。

梯度下降算法:
目的:寻找代价函数最小时的参数
方法:找到梯度最大的方向
结果:局部最优解
注意:同步更新