第四次实验

问题 E: 深入浅出学算法100-组合的输出

题目描述

排列与组合是常用的数学方法，其中组合就是从n个元素中抽出r个元素(不分顺序且r<＝n)，我们可以简单地将n个元素理解为自然数1，2，…，n，从中任取r个数。

    现要求你用递归的方法输出所有组合。

    例如n＝5，r＝3，所有组合为：

    l 2 3   l 2 4   1 2 5   l 3 4   l 3 5   1 4 5   2 3 4   2 3 5   2 4 5   3 4 5

输入:一行两个自然数n、r(1<n<21，1<＝r<＝n)。

输出:   所有的组合，每一个组合占一行且其中的元素按由小到大的顺序排列，每个元素占三个字符的位置（右对齐），所有的组合也按字典顺序。

样例输入:5 3

样例输出 

1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5

#include<bits/stdc++.h>
using namespace std;
void search(int,int,int,int);
int a[300];
int main()
{
    int n,r;
    cin>>n>>r;//读入 
    search(1,0,n,r);//从第一个位置，现在是0，n个数字中取r个 
    return 0;
}
void search(int k,int last,int n,int m){
    if(k>m){
        for(int i=1;i<=m;++i)printf("%3d",a[i]);//占位输出换行 
        printf("
");
        return ;
    }
    for(int i=last+1;i<=n;++i){
        a[k]=i;// 往当前第k位放last+1的数值 
        search(k+1,i,n,m);//传递刚存入的i值，往第k+1位放数 
    }
}

问题 F: 深入浅出学算法101-N皇后问题

题目描述：在N*N的棋盘上放置N个皇后（n<=10）而彼此不受攻击（即在棋盘的任一行，任一列和任一对角线上不能放置2个皇后），编程求解所有的摆放方法。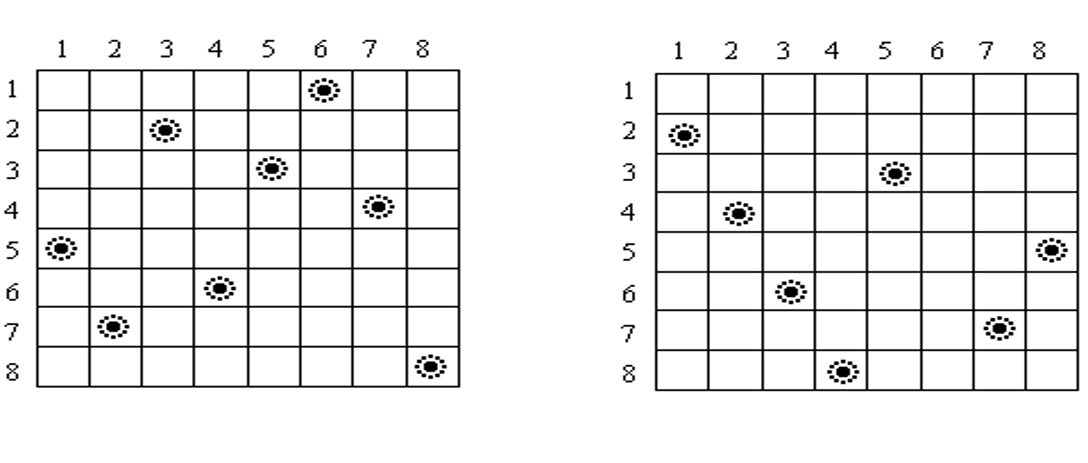

输入： n

输出：每行输出一种方案，每种方案顺序输出皇后所在的列号，每个数占5列（输出时按字典序）。若无方案，则输出no solute!

样例输入 ： 4

样例输出 ：

    2    4    1    3
    3    1    4    2

#include<bits/stdc++.h>
using namespace std;
void search(int,int,int,int);
int c[20],r[20],dz[20],df[20];//主对角线与副对角线 
int tot,ans[20];
void dfs(int now,int n);
int main(){
    memset(c,0,sizeof(c));
    memset(r,0,sizeof(r));
    memset(dz,0,sizeof(dz));
    memset(df,0,sizeof(df));
    memset(ans,0,sizeof(ans));
    int n;
    cin>>n;
    dfs(1,n);
    if(!tot)printf("no solute!");//tot统计结果数量 
    return 0;
}
void dfs(int x,int n){
    if(x>n){
        tot++;
        for(int i=1;i<=n;++i)printf("%5d",ans[i]);
        printf("
");
    }
    for(int y=1;y<=n;++y){
        if(dz[x+y]||df[x-y+10]||c[y])continue;//如果对角线或者这一行有了，那就不继续往下 
        ans[x]=y;dz[x+y]=df[x-y+10]=c[y]=1;
        dfs(x+1,n);
        dz[x+y]=df[x-y+10]=c[y]=0;//回溯 
    }
}

对角线判断忘掉了，深度优先搜索判断对角线是否有元素的问题 点这个链接参考博客。

问题 H: 深入浅出学算法109-最佳调度问题

题目描述：假设有n个任务由k个可并行工作的机器完成。完成任务i需要的时间为ti。试设计一个算法找出完成这n个任务的最佳调度，使得完成全部任务的时间最早。

输入：第一行有2 个正整数n和k。第2 行的n个正整数是完成n个任务需要的时间。

输出：计算出的完成全部任务的最早时间 

样例输入 

7  3
2  14  4  16  6  5  3

样例输出 ：17

#include<bits/stdc++.h>
using namespace std;

int ans=0x3f3f3f;
int sum[1010],a[1010];
void dfs(int now,int nows,int n,int k){//目前是第now个任务，已花费nows时间 
    if(ans<=nows)return ;//如果不比现在最小的结果小，就停止搜索 
    if(now==n+1){
        ans = min(ans,nows);//搜到底，更新数据 
        return ;
    }
    for(int i=1;i<=k;++i){
        if(sum[i]+a[now]<ans){
            sum[i]+=a[now];
            dfs(now+1,max(sum[i],nows),n,k);
            sum[i]-=a[now];//回溯 
        }
    }
    return ;
}
bool cmp(int a,int b){
    return a>b;
}
int main(){
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;++i)cin>>a[i];
    sort(a+1,a+1+n,cmp);//从大到小排序，从逻辑上来说，排队的时候，运行时长最大的优先，能让总体等待时间最短 
    sum[1]=a[1]; 
    dfs(2,a[1],n,k);
    cout<<ans<<endl; 
}