什么是Merkle Tree?
Merkle Tree 的命名来自于美国密码学家Ralph C. Merkle ,关于他的个人资料:传送门https://en.wikipedia.org/wiki/Ralph_Merkle。与前面讲的几种算法不同,Merkle Tree是一种树结构,而并非具体的某种算法。
在具体讲之前,简单说一下哈希算法:
哈希算法是密码学中一种基础的算法,通常的特点:
1.任意的输入值经过哈希算法都能产生固定长度的输出。
2.输入值的微小变化都能导致输出值的巨大变化。
优秀的哈希算法通常还包括不能根据输入推算出输出。这在SHA256中有过介绍。那么Merkle Tree通常也被称做Hash Tree,实际上一个Merkle Tree就是由hash值构成的树结构,可以是二叉树,也可以多叉树,无论是几叉树,它都具有树结构的所有特点;
下面这张图就是一个典型的Merkle Tree:
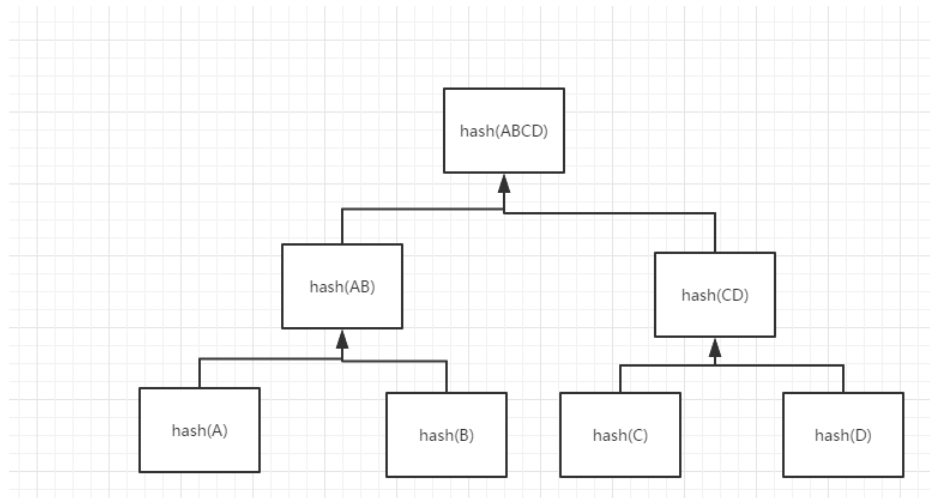

通过对A进行hash运算得到的值和B经过一样哈希得到的值在进行一次哈希运算,层层网上,最后只有一个Top hash值。这个值就被称为 merkle root,摩尔根。
Merkle Tree在区块链中的应用
在比特币中,Merkle Tree的每个节点的值都是通过两次SHA256算法得到的:
HA = SHA256(SHA256(Transaction A)),HB = SHA256(SHA256(Transaction B)),
那么HA&B 就是对HA和HB串联起来在进行两次SHA256算法。关于SHA256算法可以学习本系列的第一篇。
都知道区块链是一个个区块连起来的结果,下面是比特币中一个区块的结构:


每个摩尔根是多个交易的集合,区块链中每个摩尔根的值都是唯一的。除此之外,merkle树还提供了一种在比特币网络中快速校验某个交易是否存在的有效途径。
spv节点中merkle的应用
比特币网络中并不是每个节点都包含了全网所有的数据,为了简化支付验证,比特币中存在一种spv节点,该节点不需要备份所有的数据就能验证一笔交易。我们的手机/pad/电脑上安装的很多钱包软件都属于spv节点。spv节点没有存储全网的区块链数据,但是存储了所有的去块头,这就类似于书架上没有存所有的书的内容,但是存储了所有的书的章节目录。SPV节点会收到少于1KB的有关区块头和Merkle路径的数据,其数据量比一个完整的区块(目前大约有1MB)少了一千多倍。减少了存储,又保有了交易的验证资格。
SPV负责判断该交易是否已经得到区块链的节点共识认证以及多少次确认。
比方说想验证下面的H(K)交易是否支付完成:

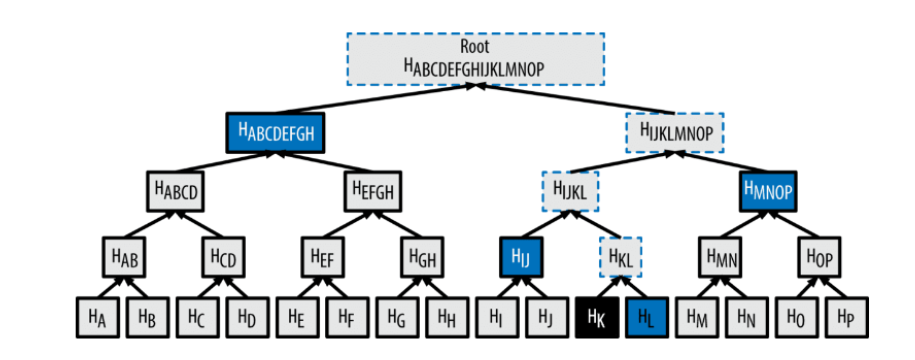
首先,节点从网络上获取需要验证的交易的认证路径,在节点上生成对应的一个路径,该路径的值就是图中蓝色标示的节点。在路径确认的情况下,节点只需要计算H(KL)、H(IJKL)、H(IJKLMNOP),H(ABCDEFGHIJKLMNOP)的两次hash值,这样得到的一个摩尔根的副本。前面讲过spv节点保存了整个区块链的所有去块头,所以只要拿这个副本和去块头中的摩尔根比较。如果存在就能证明该交易支付成功。
Merkle Tree在其他领域的应用
早在区块链出现之前摩尔树就在各个领域中得到了应用。列如文件下载,目前通常采用HASH值直接验证。但是如果下载的文件比较大,那么用户就需要知道是什么地方的文件下载出错,直接重新下载出错的部分而不需要重新下载全部文件,节省了大量的时间。还有在数字签名上的应用,git版本控制,eth。本质来讲,摩尔根树是通过一个优秀的hash算法不可逆的特性来设计出的一个树结构,在验证某个节点是否存在时节省了大量的计算。由此可见,一些优秀的方法应用并不是需要特别专业的技能,而是需要敏锐的观察和结合知识的能力。所以我们期待,密码学这座宝山,正在熠熠闪光等着广大从业者去开采。