今日头条2018校招大数据/算法方向（第一批）详解

第一题：

P为给定的二维平面整数点集。定义 P 中某点x，如果x满足 P 中任意点都不在 x 的右上方区域内（横纵坐标都大于x），则称其为“最大的”。求出所有“最大的”点的集合。（所有点的横坐标和纵坐标都不重复, 坐标轴范围在[0, 1e9) 内）

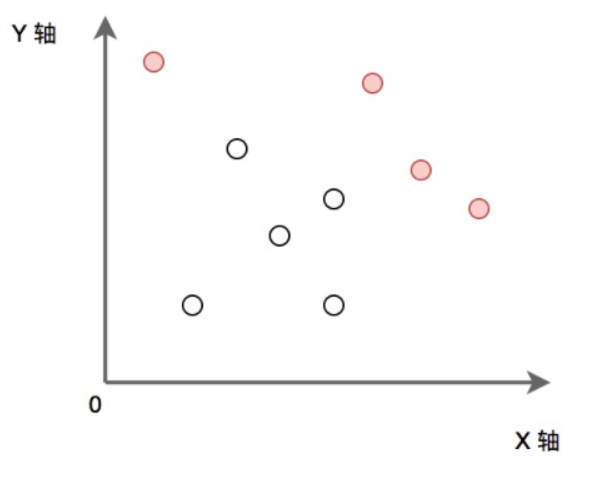
如下图：实心点为满足条件的点的集合。请实现代码找到集合 P 中的所有 ”最大“ 点的集合并输出。

 题解：

要找到所有“最大”的点，要求是右上方无其他点。

考虑从最大x坐标往左搜索，此时第一个点肯定是最右边的且此时其上方也无其他点。后面每循环到的点，右边是已循环过的点，此时需判断当前点的y坐标是否高于已循环过的最大y坐标，若大于则是“最大”点。

#内存超限，写法不简短
n = int(input())
class point():
    def __int__(self):
        self.x, self.y = -1, -1
    def toS(self):
        return self.x,self.y
p_list = []
for i in range(n):
    t = input()
    p = point()
    tx, ty = t.split(' ')
    p.x, p.y = int(tx), int(ty)
    p_list.append(p)
p_list = sorted(p_list, key=lambda point: point.x, reverse=True)
now = -1
ep = []
for i in range(n):
    if p_list[i].y > now:
        p = point()
        p.x, p.y = p_list[i].x, p_list[i].y
        now = p_list[i].y
        ep.append(p)
ep = sorted(ep, key=lambda point: point.x)
for p in ep:
    print(str(p.x) + ' ' + str(p.y))

#内存超限，从y轴开始搜索，比较x值；写法简便
n = int(input())
p_list = []
for _ in range(n):
    x, y = [int(x) for x in input().split()]
    p_list.append((x,y))
p_list = sorted(p_list, key=lambda x: x[1], reverse=True)
max_x = float('-inf')
for x, y in p_list:
    if x > max_x:
        print(x, y)
        max_x = x

//AC代码
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 500010;
struct point {
    int x, y;
}st[maxn],ed[maxn];
bool cmp(point a, point b) {
    return a.x > b.x;
}
int main(){
    int n;
    cin >> n;
    for( int i = 0; i < n; i ++ ) {
        cin >> st[i].x >> st[i].y;
    }
    sort(st,st+n,cmp);
    int now = -1, cnt = 0;
    for( int i = 0; i < n; i ++ ) {
        if( now < st[i].y ) {
            now = st[i].y;
            ed[cnt].x = st[i].x, ed[cnt].y = st[i].y;
            cnt ++;
        }
    }
    sort(ed,ed+n,cmp);
    for( int i = cnt-1; i >= 0; i -- ) {
        cout << ed[i].x << " " << ed[i].y << endl;
    }
    return 0;
}

第二题：

给定一个数组序列, 需要求选出一个区间, 使得该区间是所有区间中经过如下计算的值最大的一个：

区间中的最小数 * 区间所有数的和最后程序输出经过计算后的最大值即可，不需要输出具体的区间。如给定序列  [6 2 1]则根据上述公式, 可得到所有可以选定各个区间的计算值:

 

[6] = 6 * 6 = 36;

[2] = 2 * 2 = 4;

[1] = 1 * 1 = 1;

[6,2] = 2 * 8 = 16;

[2,1] = 1 * 3 = 3;

[6, 2, 1] = 1 * 9 = 9;

 

从上述计算可见选定区间 [6] ，计算值为 36， 则程序输出为 36。

区间内的所有数字都在[0, 100]的范围内;

题解：

求区间最大值。最大值为最小值乘以区间和。

考虑确定最小值的时候，区间和越大则区间最大值越大。所以求区间最大值可以转变为找区间最小值。

遍历区间找到最小值，然后比较此时最小值确定时的最大值、最小值左边区间最大值、最小值右边区间最大值三者的大小。

搜索左边、右边至单个元素被搜索到，比较所有值确定最大值。

//AC代码，算了一下我认为计算可能超int，便使用了long long
#include<iostream>
#include<algorithm>
using namespace std;
int maxn = 500010;
long long findn( int left, int right, long long a[] ) {
    if( left >= right ) {
        return 0;
    }
    int minn = 101, mid;
    long long sum = 0;
    for( int i = left; i < right; i ++ ) {
        if( minn > a[i] ) {
            minn = a[i];
            mid = i;
        }
        sum += a[i];
    }
    return max(sum*minn,max(findn(left,mid,a),findn(mid+1,right,a)));
}
int main(){
    long long n, a[maxn];
    cin >> n;
    for( int i = 0; i < n; i ++ ) {
        cin >> a[i];
    }
    cout << findn(0,n,a) << endl;
    return 0;
}

第三题

产品经理(PM)有很多好的idea，而这些idea需要程序员实现。现在有N个PM，在某个时间会想出一个 idea，每个 idea 有提出时间、所需时间和优先等级。对于一个PM来说，最想实现的idea首先考虑优先等级高的，相同的情况下优先所需时间最小的，还相同的情况下选择最早想出的，没有 PM 会在同一时刻提出两个 idea。

同时有M个程序员，每个程序员空闲的时候就会查看每个PM尚未执行并且最想完成的一个idea,然后从中挑选出所需时间最小的一个idea独立实现，如果所需时间相同则选择PM序号最小的。直到完成了idea才会重复上述操作。如果有多个同时处于空闲状态的程序员，那么他们会依次进行查看idea的操作。

求每个idea实现的时间。

输入第一行三个数N、M、P，分别表示有N个PM，M个程序员，P个idea。随后有P行，每行有4个数字，分别是PM序号、提出时间、优先等级和所需时间。输出P行，分别表示每个idea实现的时间点。

题解：

PM的最想完成idea是优先级最大的idea，优先级相同时时所需时间最小的。每个程序员空闲时是从所有PM最想完成的idea中挑选所需时间最小的完成，时间相同选择PM序号最小。

考虑使用一个优先级队列数组，存每个PM想完成的idea，按题目规则排序。再使用一个优先级队列存每个程序员已花费时间。

注意：存在的特殊情况是程序员空闲但时间未到PM任务的开始时间。此时增加优先级队列中程序员的时间。

参考：https://www.kanzhun.com/jiaocheng/584615.html

//AC代码
#include<queue>
#include<vector>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 3010;
struct node {
    int pm, st, prior, cost, index;
};
struct cmpStruct {
    bool operator()( node a, node b ) {
        if( a.prior != b.prior ) {
            return a.prior < b.prior;
        } else if( a.cost != b.cost ) {
            return a.cost > b.cost;
        } else if( a.st != b.st ) {
            return a.st > b.st;
        }
        return a.pm > b.pm;
    }
};
bool cmp( node a, node b ) {
    return a.st < b.st;
}
int main() {
    int ans[maxn];
    node no[maxn];
    vector<node> vec[maxn];
    priority_queue<node, vector<node>, cmpStruct> q[maxn];
    priority_queue<int, vector<int>, greater<int> > q_time;
    int n, m, p;
    cin >> n >> m >> p;
    for( int i = 0; i < p; i ++ ) {
        cin >> no[i].pm >> no[i].st >> no[i].prior >> no[i].cost;
        no[i].index = i+1;
    }
    sort(no,no+p,cmp);
    int task_start_id = 0;
    for( int i = 0; i < m; i ++ ) {
        q_time.push(1);
    }
    int start_time = q_time.top();
    int task_finish_cnt = 0;
    while( 1 ) {
        int i = task_start_id;
        for( ; i < p; i ++ ) {
            if( no[i].st <= start_time ) {
                q[no[i].pm].push(no[i]);
            } else {
                break;
            }
        }
        task_start_id = i;
        q_time.pop();
        int minn = maxn, pm_id = 0;
        for( int i = 1; i <= n; i ++ ) {
            if( !q[i].empty() && q[i].top().cost < minn ) {
                minn = q[i].top().cost;
                pm_id = i;
            }
        }
        if( pm_id > 0 ) {
            int finish_time = start_time + q[pm_id].top().cost;
            ans[q[pm_id].top().index] = finish_time;
            task_finish_cnt ++;
            if( task_finish_cnt == p ) {
                break;
            }
            q_time.push(finish_time);
            q[pm_id].pop();
        } else {
            q_time.push(start_time+1);
        }
        start_time = q_time.top();
    }
    for( int i = 1; i <= p; i ++ ) {
        cout << ans[i] << endl;
    }
    return 0;
}

第四题

给定一棵树的根节点, 在已知该树最大深度的情况下, 求节点数最多的那一层并返回具体的层数。

如果最后答案有多层, 输出最浅的那一层，树的深度不会超过100000。实现代码如下，请指出代码中的多处错误：

参考：https://blog.csdn.net/f_zyj/article/details/79162401

struct Node {

    vector<Node*> sons;

};

 

void dfsFind(Node *node, int dep, int counter[]) {

    counter[dep]++;

 

    for(int i = 0; i < node.sons.size(); i++) {

        dfsFind(node.sons[i], dep, counter);

    }

}

 

int find(Node *root, int maxDep) {

    int depCounter[100000];

    dfsFind(root, 0, depCounter);

 

    int max, maxDep;

    for (int i = 1; i <= maxDep; i++) {

        if (depCounter[i] > max) {

            max = depCounter[i];

            maxDep = i;

        }

    }

    return maxDep;

}

/*
 *  Node 结构体，包含一个元素为 Node * 的向量
 *  用来存储树结构的父子关系
 */
struct Node {
    vector<Node*> sons;
};

/*
 *  深度优先遍历，用来遍历树并且对每层结点数计数
 *  node 为父节点的指针，dep 为深度，counter 为存储每层结点数的数组
 */
void dfsFind(Node *node, int dep, int counter[]) {
    counter[dep]++;                                 //  计数操作
    for(int i = 0; i < node->sons.size(); i++) {    //  错误 1 指针操作错误
        dfsFind(node->sons[i], dep + 1, counter);   //  错误 2 指针操作错误，深度控制不当
    }
}

/*
 *  find 函数，root 是树的根，maxDep 是树的最大深度
 */
int find(Node *root, int maxDep) {
    int depCounter[100003];               //  错误 3 存储树的每层结点数.可能存在越界问题
    dfsFind(root, 0, depCounter);         //  调用深度优先遍历函数，
                                          //  传入根和初始深度以及存储数每层结点数的数组
    int max = 1, res = 0;                 //  错误 4 未初始化、命名冲突
    for (int i = 1; i <= maxDep; i++) {    
        if (depCounter[i] > max) {
            max = depCounter[i];
            res = i;                      //  错误 5 被赋值变量错误
        }
    }
    return res;                           //  错误 6 返回错误变量
}

第五题

早期短链接广泛应用于图片上传网站，通过缩短网址URL链接字数，达到减少代码字符串的目的。常见于网店图片分类的使用，因有字符个数限制，采用短链接可以达到外链图片的目的。自微博盛行以来，在微博字数有限的特色下，短链接也盛行于微博网站，以节省字数给博主发布更多文字的空间。

问题描述：设计一个短链生成和查询系统，需要提供以下两个功能：

    1、提供长链转换短链的接口

    2、点击短链能跳转到对应的长链

题目要求：

    1、同一个长链生成同一个短链接，不要有多个短链指向同一个长链。

    2、同一个短链只能指向某一个长链，短链生成后要固定不变，不能再指向其它长链。

    3、给出系统架构，需要考虑高并发解决方案。

    4、考虑存储和缓存方案

数据量预估：

    1、预计长链接总量500亿

    2、长链换短链请求量：10W qps

    3、短链跳转请求量：100W qps

 

题解：

设计：
1、长链转短链
发号器，每过来一个长链换短链请求发一个号，发号器所发号码从 0 自增，所发号码为十进制，转化为 62进制后作为短链（62 进制对应 26 小写字母加上 26大写字母还有 10 数字）。
2、短链跳转长链
将短链所对应号码与长链一一映射存储于表中。

优化：
1、长链对应唯一短链
当长链转短链请求过来时率先在字典树（映射）中查找该长链是否已经分配短链，如果分配，则直接返回短链，若未分配则利用发号器继续分配。字典树在发号同时建立。
2、系统架构与高并发
采用 key−value 分布式储存系统，创建更多发号器，减小发号请求高并发时的压力，比方说创建 10000 个发号器，1发号器发号从 0∼9999，2发号器发号从10000~19999依次类推，每个发号器对应一片内存存储所发号码与长链对应的表，减小跳转访问高并发时的压力。
3、存储和缓存
利用分布式系统，采用 NoSql 数据库存储彼此一一映射，采用 LRU算法管理内存与缓存。
参考：https://blog.csdn.net/f_zyj/article/details/79162401

附上：短网址系统如何实现？