数据结构之Set | 让我们一块来学习数据结构

数组（列表）、栈、队列和链表这些顺序数据结构对你来说应该不陌生了。现在我们要学习集合，这是一种不允许值重复的顺序数据结构。我们将要学到如何创建集合这种数据结构，如何添加和移除值，如何搜索值是否存在。你也会学到如何进行并集、交集、差集等数学运算。

本章内容包括：

• 从头创建一个 Set 类
• 用 Set 来进行数学运算

构建数据集合

集合是由一组无序且唯一（即不能重复）的项组成的。该数据结构使用了与有限集合相同的数学概念，但应用在计算机科学的数据结构中。

在深入学习集合的计算机科学实现之前，我们先看看它的数学概念。在数学中，集合是一组不同对象的集。

比如说，一个由大于或等于 0 的整数组成的自然数集合：N = {0, 1, 2, 3, 4, 5, 6, …}。集合中的对象列表用花括号（{}）包围。

还有一个概念叫空集。空集就是不包含任何元素的集合。比如 24 和 29 之间的素数集合，由于 24 和 29 之间没有素数（除了 1 和自身，没有其他正因数的、大于 1 的自然数），这个集合就是空集。空集用{ }表示。

你也可以把集合想象成一个既没有重复元素，也没有顺序概念的数组。在数学中，集合也有并集、交集、差集等基本运算。本文也会介绍这些运算。

创建集合类

创建基础类

用下面的 Set 类以及它的构造函数声明作为开始。

class Set {
    constructor() {
        this.items = {};
    }
}

有一个非常重要的细节是，我们使用对象而不是数组来表示集合（items）。不过，也可以用数组实现。此处用对象来实现，和我们在第 4 章与第 5 章中学习到的对象实现方式很相似。同样地，JavaScript 的对象不允许一个键指向两个不同的属性，也保证了集合里的元素都是唯一的。

接下来，需要声明一些集合可用的方法（我们会尝试模拟与 ECMAScript 2015 实现相同的Set 类）。

• add(element)：向集合添加一个新元素。
• delete(element)：从集合移除一个元素。
• has(element)：如果元素在集合中，返回 true，否则返回 false。
• clear()：移除集合中的所有元素。
• size()：返回集合所包含元素的数量。它与数组的 length 属性类似。
• values()：返回一个包含集合中所有值（元素）的数组。

has(item)方法

首先要实现的是 has(element)方法，因为它会被 add、delete 等其他方法调用。它用来检验某个元素是否存在于集合中，下面看看它的实现。

has(item) {
    return Object.prototype.hasOwnProperty.call(this.items, item);
}

除了使用Object.prototype.hasOwnProperty方法实现之外，还可以使用item in this.items和this.items.hasOwnProperty(item)来实现has方法。

add(item)方法

接下来要实现 add(item) 方法。

add(item) {
    if (this.has(item)) {
        return false;
    }
    this.items[item] = item;
    return true;
}

对于给定的 item，可以检查它是否存在于集合中。如果不存在，就把 item 添加到集合中，并返回 true，表示添加了该元素。如果集合中已经有了这个元素，就返回 false，表示没有添加它。

delete(item) 和 clear() 方法

下面要实现 delete(item) 方法。

delete(item) {
    if (this.has(item)) {
        delete this.items[item];
        return true
    }
    return false
}

在 delete 方法中，我们会验证给定的 item 是否存在于集合中。如果存在，就从集合中移除 item，返回 true，表示元素被移除；否则返回 false。

由于我们是使用对象来存储集合的items对象，那么就可以简单的使用对象的delete运算符从items中删除元素。

如果想移除集合中的所有值，可以用 clear 方法。

clear() {
    this.items = {}
}

size() 方法

实现size方法有几种方式：

1. 使用一个 length 变量，每当使用 add 或 delete 方法时就控制它
2. Object.keys(this.items).length
3. 使用for in (要记得使用hasOwnProperty判断一下)
4. ...

现在我们使用第2中方式来实现，代码如下

size() {
    return Object.keys(this.items).length;
}

values() 方法

要实现 values() 方法，我们同样可以使用 Object 类内置的 values 方法。

values() {
    return Object.values(values); 
}

Object.values()方法返回了一个包含给定对象所有属性值的数组。它是在ECMAScript 2017 中被添加进来的，目前只在现代浏览器中可用。

使用Set类

现在数据结构已经完成了，看看如何使用它吧。试着执行一些命令，测试我们的 Set 类。

const set = new Set(); 
set.add(1); 
console.log(set.values()); // 输出[1] 
console.log(set.has(1)); // 输出 true 
console.log(set.size()); // 输出 1 
set.add(2); 
console.log(set.values()); // 输出[1, 2] 
console.log(set.has(2)); // 输出 true 
console.log(set.size()); // 输出 2 
set.delete(1); 
console.log(set.values()); // 输出[2] 
set.delete(2); 
console.log(set.values()); // 输出[] 

集合运算

集合是数学中基础的概念，在计算机领域也非常重要。它在计算机科学中的主要应用之一是数据库，而数据库是大多数应用程序的根基。集合被用于查询的设计和处理。当我们创建一条从关系型数据库（Oracle、Microsoft SQL Server、MySQL 等）中获取一个数据集合的查询语句时，使用的就是集合运算，并且数据库也会返回一个数据集合。当我们创建一条 SQL 查询命令时，可以指定是从表中获取全部数据还是获取其中的子集；也可以获取两张表共有的数据、只存在于一张表中的数据（不存在于另一张表中），或是存在于两张表内的数据（通过其他运算）。这些 SQL 领域的运算叫作联接，而 SQL 联接的基础就是集合运算。

我们可以对集合进行如下运算。

• 并集：对于给定的两个集合，返回一个包含两个集合中所有元素的新集合。
• 交集：对于给定的两个集合，返回一个包含两个集合中共有元素的新集合。
• 差集：对于给定的两个集合，返回一个包含所有存在于第一个集合且不存在于第二个集合的元素的新集合。
• 子集：验证一个给定集合是否是另一集合的子集。

重要的是要注意，本文实现的 union、intersection 和 difference 方法不会修改当前的 Set 类实例或是作为参数传入的 otherSet。没有副作用的方法和函数被称为纯函数。纯函数不会修改当前的实例或参数，只会生成一个新的结果。这在函数式编程中是非常重要的概念。

并集

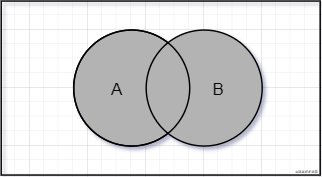
并集的数学概念。集合 A 和集合 B 的并集表示为 (A ∪ B)，定义如下。

[A ∪ B = { x ∣ x ∈ A ∨ x ∈ B } ]

意思是 x（元素）存在于 A 中，或 x 存在于 B 中。下图展示了并集运算。

代码实现

union(otherSet) {
    let unionSet = new Set();
    let values = this.values();
    values.forEach((value) => {
        unionSet.add(value);
    });
    values = otherSet.values();
    values.forEach((value) => {
        unionSet.add(value);
    });
    return unionSet;
}

交集

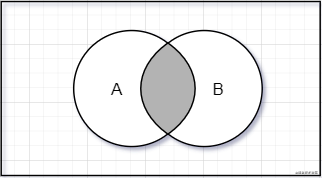
交集的数学概念。集合 A 和集合 B 的交集表示为 (A ∩ B)，定义如下。

[A ∩ B = { x ∣ x ∈ A ∧ x ∈ B } ]

意思是 x（元素）存在于 A 中，且 x 存在于 B 中。下图展示了交集运算。

代码实现

intersection(otherSet) {
    let intersectionSet = new Set();
    const values = this.values();
    const otherValues = otherSet.values();
    let smallerValues = values;
    let biggerValues = otherValues;
    if (otherValues.length < values.length) {
        smallerValues = otherValues;
        biggerValues = values;
    }
    smallerValues.forEach((value) => {
        if (biggerValues.includes(value)) {
            intersectionSet.add(value);
        }
    });
    return intersectionSet;
}

> 为了减少循环次数，在代码中判断了哪个集合的长度最小，然后循环长度较小的集合，以达到减少循环次数的目的。

差集

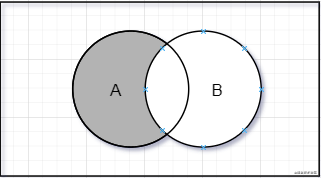
差集的数学概念。集合 A 和集合 B 的差集表示为 (A - B)，定义如下。

[A ∪ B = { x ∣ x ∈ A ∧ x ∉ B } ]

意思是 x（元素）存在于 A 中，且 x 不存在于 B 中。下图展示了集合 A 和集合 B 的差集运算。

代码实现

difference(otherSet) {
    let differenceSet = new Set();

    this.values().forEach((value) => {
        if (!otherSet.has(value)) {
            differenceSet.add(value);
        }
    });
    return differenceSet;
}

子集

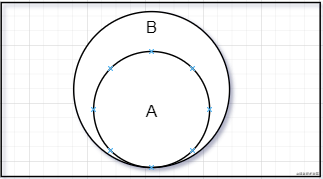
要介绍的最后一个集合运算是子集。其数学概念的一个例子是集合 A 是集合 B 的子集（或集合 B 包含集合 A），表示为 (A ∈ B)，定义如下。

[A ∪ B = { x ∣ ∀x ∈ A => x ∈ B } ]

意思是集合 A 中的每一个 x（元素），也需要存在于集合 B 中。下图展示了集合 A 是集合 B 的子集。

代码实现

isSubsetOf(otherSet) {
    if (this.size() > otherSet.size()) {
        return false;
    }
    let isSubset = true;
    const values = this.values();
    const size = this.size();
    for (let i = 0; i < size; i++) {
        if (!otherSet.has(values[i])) {
            isSubset = false;
            break;
        }
    }
    return isSubset;
}

参考资料

• 学习JavaScript数据结构与算法第三版

其它数据结构的文章

• 数据结构之LinkedList | 让我们一块来学习数据结构
• 数据结构之List | 让我们一块来学习数据结构
• 数据结构之Stack | 让我们一块来学习数据结构
• 数据结构之Queue | 让我们一块来学习数据结构