判断一颗二叉树是不是完全二叉树【Java】

思路

　　完全二叉树和非完全二叉树的最大的区别就是完全二叉树的叶子节点只能在最后一层后者倒数第二层，其他层其实是一个满二叉树，而且最后一层的叶子节点都要靠近最左边。

如图：

　　

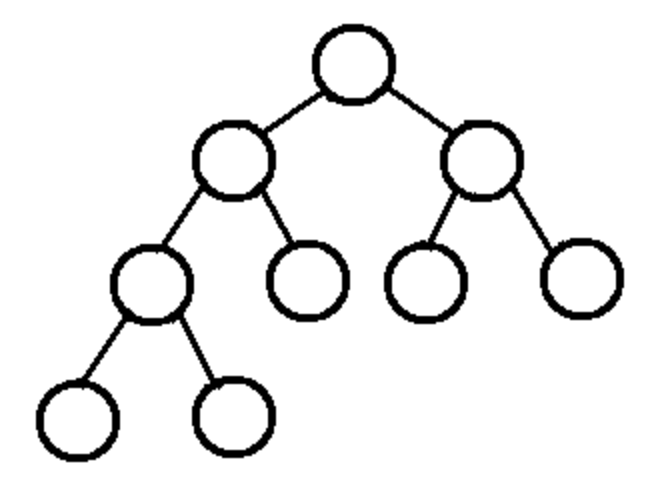
二叉树的构成代码和节点代码

二叉树：

package com.example.demo.tree;

import com.sun.scenario.effect.impl.sw.sse.SSEBlend_SRC_OUTPeer;
import org.omg.PortableInterceptor.INACTIVE;

import java.util.Comparator;

/**
 * @author steve
 * @date 2020/4/16 10:03 上午
 */
public class BinaryTree<E> {

    private int size;
    public Node<E> root;
    private Comparator<E> comparator;

    public BinaryTree(Comparator<E> comparator){
        this.comparator = comparator;
    }

    public BinaryTree(){
        this(null);
    }

    public void add(E element){
        if (root == null){
            Node node = new Node(element);
            root = node;
        }else {
            Node<E> parent = root;
            Node<E> node = root;
            int com = 0;
            while (node != null){
                parent = node;
                if (comparator == null){
                    com = ((Comparable)node.element).compareTo(element);
                }else {
                    System.out.println("-------------");
                    com = comparator.compare(node.element,element);
                }
                if (com > 0){
                    node = node.left;
                }else if (com < 0){
                    node = node.right;
                }else {
                    node.element = element;
                    return;
                }
            }
            Node<E> newNode = new Node(element);
            if (com > 0){
                parent.left = newNode;
                newNode.parent = parent.left;
            }else{
                parent.right = newNode;
                newNode.parent = parent.right;
            }
        }
        size ++;
    }
    public boolean isEmpty(){
        return size == 0;
    }
    public int size(){
        return size;
    }

    public String toString() {
        String d = root == null ? null : root.element + "";
        if (root == null){
            return "root:"+d;
        }else {
            String b = root.left == null ? null : root.left.element + "";
            String c = root.right == null ? null : root.right.element + "";
            return "root:"+d + ", left:" + b + ", right:"+ c;
        }

    }


    public static void main(String[] args) {
        //这种方式就是匿名内部类，通过给一个类传一个接口作为参数，然后这个通过一个匿名内部类是实现这个接口来传入实现。
        BinaryTree<Integer> binaryTree = new BinaryTree<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1 - o2;
            }
        });

        BinaryTree<Integer> binaryTree1 = new BinaryTree<>();
        binaryTree1.add(1);
        binaryTree1.add(2);
        binaryTree1.add(0);
        System.out.println(binaryTree1.size());
        System.out.println(binaryTree.toString());
    }
}

节点：

package com.example.demo.tree;

/**
 * @author steve
 * @date 2020/4/18 3:16 下午
 */
public class Node<E> {
    public Node<E> left;
    public Node<E> right;
    public Node<E> parent;
    public E element;
    public Node(E element){
        this.element = element;
    }
}

判断二叉树是不是完全二叉树

package com.example.demo.tree;

import java.util.LinkedList;
import java.util.Queue;

/**
 * @author steve
 * @date 2020/4/20 8:31 下午
 * 判断是不是完全二叉树,采用层序遍历的方式
 * 判断依据：如果某个节点没有左子树或者右子树，就直接结束二叉树遍历，这时候队列可能并不为空，
 * 但是队列中的节点必须都是叶子节点，否则就不是完全二叉树
 */
public class JudgeFullBinaryTree {

    public static void judge(Node<Integer> node){
        Queue<Node<Integer>> queue = new LinkedList<>();
        queue.add(node);
        boolean flag = true;
        while(!queue.isEmpty()){
            //这里没有直接使用queue.poll()的原因是，如果最后那个节点没有左子树，但是有右子树，那么这个循环也会停止，
            //而且那个节点也会从队列中弹出，如果刚好是那个节点就是问题节点，那最后的结果就是有问题的，所以这里使用peek
            node = queue.peek();
            //遇见为空的直接停止
            if (node.left != null){
                queue.add(node.left);
            }else {
                break;
            }
            //遇见为空直接停止
            if (node.right != null){
                queue.add(node.right);
            }else {
                break;
            }
            queue.poll();
        }
        //这里搞这个判断的原因，就是看一下暂停遍历的那个节点是不是有问题，因为上面的循环并没有把这个节点弹出
        if (queue.peek().right == null){
            queue.poll();
        }
        //这里判断队列中剩余的节点是不是都是叶子节点
        while (!queue.isEmpty()){
            node = queue.poll();
            if (node.left != null || node.right != null){
                flag = false;
            }
        }
        System.out.println(flag);
    }

    /**
     *                    7
     *                   / 
     *                  4   10
     *                 /   /
     *                3  5 9  11
     *               /
     *              1
     *             /
     *            0
     * @param args
     */
    public static void main(String[] args) {
        BinaryTree<Integer> binaryTree = new BinaryTree();
        binaryTree.add(7);
        binaryTree.add(4);
        binaryTree.add(10);
        binaryTree.add(9);
        binaryTree.add(11);
        binaryTree.add(5);
        binaryTree.add(3);
        binaryTree.add(1);
        binaryTree.add(0);
        judge(binaryTree.root);
    }

}