概念
一棵二叉树由根结点、左子树和右子树三部分组成,若规定 D、L、R 分别代表遍历根结点、遍历左子树、遍历右子树,则二叉树的遍历方式有 6 种:DLR、DRL、LDR、LRD、RDL、RLD。由于先遍历左子树和先遍历右子树在算法设计上没有本质区别,所以,只讨论三种方式:
DLR--前序遍历(根在前,从左往右,一棵树的根永远在左子树前面,左子树又永远在右子树前面 )
LDR--中序遍历(根在中,从左往右,一棵树的左子树永远在根前面,根永远在右子树前面)
LRD--后序遍历(根在后,从左往右,一棵树的左子树永远在右子树前面,右子树永远在根前面)
定理
1、二叉树的前序遍历序列一定是该树的根节点
2、中序遍历序列中根节点前面一定是该树的左子树,后面是该树的右子树
例题
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
解析
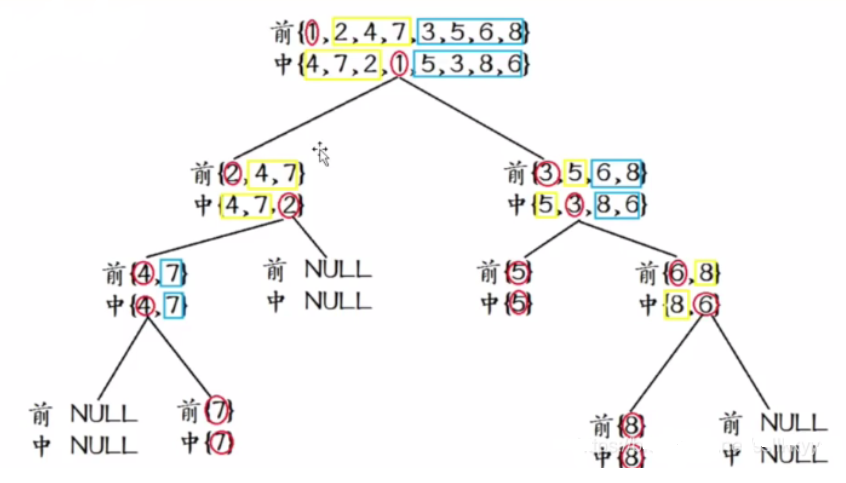
从上面可知,题目中前序遍历的第一个节点{1}一定是这棵二叉树的根节点,根据中序遍历序列,可以发现中序遍历序列中节点{1}之前的{4,7,2}是这棵二叉树的左子树,{5,3,8,6}是这棵二叉树的右子树。然后,对于左子树,递归地把前序子序列{2,4,7}和中序子序列{4,7,2}看成新的前序遍历和中序遍历序列。此时,对于这两个序列,该子树的根节点是{2},该子树的左子树为{4,7}、右子树为空,如此递归下去(即把当前子树当做树,又根据上述步骤分析)。{5,3,8,6}这棵右子树的分析也是这样。
代码
1 class TreeNode {
2 int val;
3 TreeNode left;
4 TreeNode right;
5
6 TreeNode(int x) {
7 val = x;
8 }
9 }
10
11 public class TestRecoverBinaryTree {
12 public TreeNode reConstructBinaryTree(int[] preOrder, int[] inOrder) {
13 int pLen = preOrder.length;
14 int iLen = inOrder.length;
15 if (pLen == 0 && iLen == 0) {
16 return null;
17 }
18 return btConstruct(preOrder, inOrder, 0, pLen - 1, 0, iLen - 1);
19 }
20 //构建方法,pStart和pEnd分别是前序遍历序列数组的第一个元素和最后一个元素;
21 //iStart和iEnd分别是中序遍历序列数组的第一个元素和最后一个元素。
22 public TreeNode btConstruct(int[] preOrder, int[] inOrder, int pStart, int pEnd, int iStart, int iEnd) {
23 //建立根节点
24 TreeNode tree = new TreeNode(preOrder[pStart]);
25 tree.left = null;
26 tree.right = null;
27 if (pStart == pEnd && iStart == iEnd) {
28 return tree;
29 }
30 int root = 0;
31 //找中序遍历中的根节点
32 for (root = iStart; root < iEnd; root++) {
33 if (preOrder[pStart] == inOrder[root]) {
34 break;
35 }
36 }
37 //划分左右子树
38 int leftLength = root - iStart;//左子树
39 int rightLength = iEnd - root;//右子树
40 //遍历左子树
41 if (leftLength > 0) {
42 tree.left = btConstruct(preOrder, inOrder, pStart + 1, pStart + leftLength, iStart, root - 1);
43 }
44 //遍历右子树
45 if (rightLength > 0) {
46 tree.right = btConstruct(preOrder, inOrder, pStart + leftLength + 1, pEnd, root + 1, iEnd);
47 }
48 return tree;
49 }
50 }