递归思想及几个经典题目

什么是递归

在程序中，所谓的递归，就是函数自己直接或间接的调用自己。调用自己分两种：

1. 直接调用自己

2. 间接调用自己

就递归而言最重要的就是跳出结构，因为跳出了才可以有结果.

化归思想

化归思想：将一个问题由难化易，由繁化简，由复杂化简单的过程称为化归，它是转化和归结的简称。

递归思想就是将一个问题转换为一个已解决的问题来实现

几个经典题目

斐波那契数列

斐波那契数列的排列是：0，1，1，2，3，5，8，13，21，34，55，89，144……依次类推下去，你会发现，它后一个数等于前面两个数的和。在这个数列中的数字，就被称为斐波那契数。

递归思想：一个数等于前两个数的和。(这并不是废话，这是执行思路)

首先分析数列的递归表达式： 

 

可以看到，递归写法简单优美，省去考虑很多边界条件的时间。当然，递归算法会保存很多的临时数据，类似于堆栈的过程，如果栈深太深，就会造成内存用尽，程序崩溃的现象。Java为每个线程分配了栈大小，如果栈大小溢出，就会报错，这时候还是选择递推好一点。

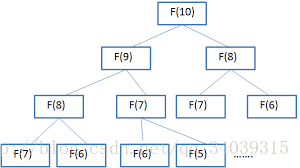
观察下面的执行过程也会发现，本程序并没有保存每次的运算结果，第三行的F(7)就执行了两次，下层的F(1),F(2)的次数更是指数级增长。这也是本程序的一个弊端。

斐波那契执行过程：

阶乘

递归思想：n! = n * (n-1)! (直接看公式吧)

首先分析数列的递归表达式： 

 

  

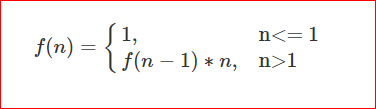
代码实现：

package 递归;

public class Test {
	public static void main(String[] args) {
		for(int i = 1;i<=10;i++){
			System.out.print(fun(i)+" "); 
			//1 2 3 5 8 13 21 34 55 89 
		}
		
		System.out.println(fun1(4)); //24
		
	}
	/*斐波那契数列的递归写法:
	 * 第三项开始，往后每一项是前两项之和。*/
//	公式：
	public static int fun(int a){
		if(a==1){ 
			return 1; 
		}else if(a==2){
			return 2; 
		}
		return fun(a-1)+fun(a-2);
	}
	
//阶乘的递归写法：
	public static int fun1(int i){
		if(i==1){
			return 1;
		}
		return i*fun1(i-1);
	}
}

　　

倒序输出一个正整数

例如给出正整数 n=12345，希望以各位数的逆序形式输出，即输出54321。

递归思想：首先输出这个数的个位数，然后再输出前面数字的个位数，直到之前没数字。

首先分析数列的递归表达式： 

 

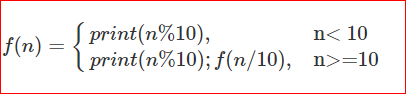
代码如下:

/**
 * 倒序输出正整数的各位数
 * @param n
 */
void printDigit(int n){
    System.out.print(n%10);
    if (n > 10){
        printDigit(n/10);
    }
}

汉诺塔

超经典了的递归解决问题了：

法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

数学描述就是：

有三根杆子X，Y，Z。X杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至Y杆： 
1. 每次只能移动一个圆盘； 
2. 大盘不能叠在小盘上面。

递归思想： 
1. 将X杆上的n-1个圆盘都移到空闲的Z杆上，并且满足上面的所有条件 
2. 将X杆上的第n个圆盘移到Y上 
3. 剩下问题就是将Z杆上的n-1个圆盘移动到Y上了

公式描述有点麻烦，用语言描述下吧： 
1. 以Y杆为中介，将前n-1个圆盘从X杆挪到Z杆上(本身就是一个n-1的汉诺塔问题了！) 
2. 将第n个圆盘移动到Y杆上 
3. 以X杆为中介，将Z杆上的n-1个圆盘移到Y杆上(本身就是一个n-1的汉诺塔问题了！)

代码如下：

/**
 * 汉诺塔
 *      有柱子 x z y，最终将x上的n个圆盘借助z移动到y上
 *      递归思想：
 *          1.将x上的n-1个放入到z上，借助y
 *          2.将x上的n圆盘放到y上
 *          3.将z上的n-1个圆盘放入y
 * @param n
 * @param from
 * @param tmp
 * @param to
 */
void hanoi(int n,char from,char tmp,char to){
    if (n>0) {
        hanoi(n - 1, from, to, tmp);
        System.out.println("take " + n + " from " + from + " to " + to);
        hanoi(n - 1, tmp, from, to);
    }
}

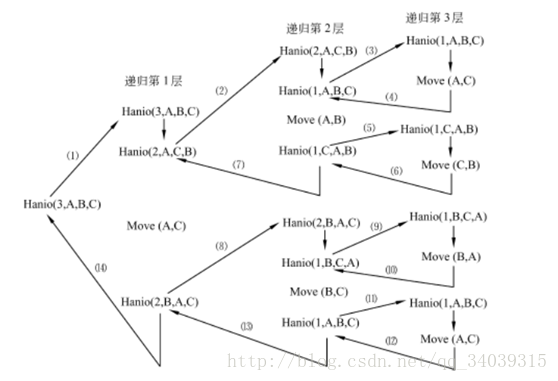
执行过程：

如果一秒钟移动一次，世界毁灭需要多长时间呢？5845.54亿年以上，而地球存在至今不过45亿年，地球现在还是很安全的。

排列问题

输入一个字符串，打印出该字符串中字符的所有排列。例如输入字符串abc，则输出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。

递归思想： 
假如针对abc的排列，可以分成 (1)以a开头，加上bc的排列 (2)以b开头，加上ac的排列 (3)以c开头，加上ab的排列

/**
 * 产生排列组合的递归写法
 * @param t     数组
 * @param k     起始排列值
 * @param n     数组长度
 */
void pai(int[] t, int k, int n){
    if (k == n-1){//输出这个排列
        for (int i = 0; i < n; i++) {
            System.out.print(t[i] + " ");
        }
        System.out.println();
    }else {
        for (int i = k; i < n; i++) {
            int tmp = t[i]; t[i] = t[k]; t[k] = tmp;//一次挑选n个字母中的一个,和前位置替换
            pai(t, k+1, n);                      //再对其余的n-1个字母一次挑选
            tmp = t[i]; t[i] = t[k]; t[k] = tmp;    //再换回来
        }
    }
}

本题用递归算法很巧妙，省去了用普通方法时保存数据状态的繁琐操作！

使用递归遍历所有的后代元素

    <script>
        //需求：给页面中所有的元素添加一个边框  1px solid pink
        //DOM中，没有提供直接获取后代元素的API,但是可以通过childNodes来获取所有的子节点
        window.onload = function () {

            //1.第一次调用时获取body的所有子元素,会把所有的子元素全部放到result里面
            //2.每放进去一个 就找这个子元素的所有子元素  有返回值
            //3.把这个返回值和我们存当前子元素的数组拼接起来 就变成了 子元素 和 孙子元素的集合

            var arr = getChildNode(document.body);
            
            for (var i = 0; i < arr.length; i++) {
                var child = arr[i];
                child.style.border= "1px solid pink";
            }

            function getChildNode(node){
                //先找子元素
                var nodeList = node.childNodes;
                var result = [];
                //在用子元素再找子元素  这里就可以递归了
                //for循环中的条件，就充当了结束的条件
                for (var i = 0; i < nodeList.length; i++) {
                    var childNode = nodeList[i];
                    //childNode获取到到的节点包含了各种类型的节点
                    //但是我们只需要元素节点  通过nodeType去判断当前的这个节点是不是元素节点
                    if(childNode.nodeType == 1){
                        result.push(childNode);
                        var temp = getChildNode(childNode);
                        result = result.concat(temp);
                    }
                }
                return result;
            }
        }
    </script>

本文大体摘自：https://blog.csdn.net/qq_34039315/article/details/78679029