本文翻译自 《Principles of training multi-layer neural network using backpropagation 》。
这篇文章讲了用反向传播(backpropagation)算法的多层神经网络训练过程。为了说明这个过程,使用了具有两个输入和一个输出的三层神经网络,如下图所示:
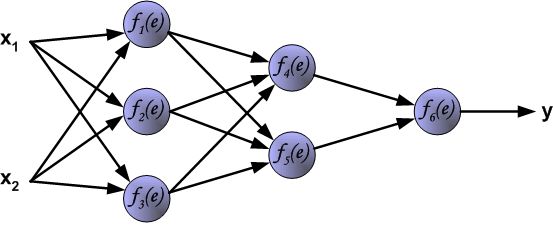
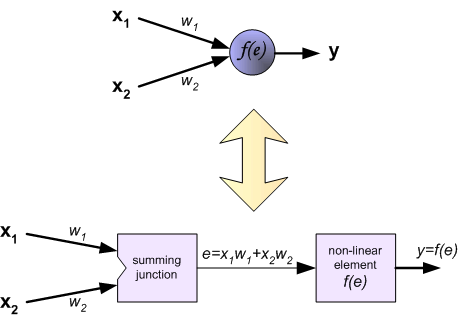
每个神经元由两个单元组成。第一单元计算所有输入信号与权重系数乘积的和。第二单元是一个非线性函数,称为神经元激活函数。信号 (e) 是加法器的输出信号, (y = f(x)) 是非线性函数的输出信号。信号 (y) 也就是神经元的输出信号。
我们需要训练数据集来训练神经网络。训练数据集由带有相应标签(期望输出) (z) 的输入信号( (x_1) 和 (x_2) )组成。网络训练是一个迭代过程。在每个迭代中,使用来自训练数据集的新数据修改节点的加权系数。使用下面描述的算法计算修改:每个教学步骤从强制来自训练集的两个输入信号开始。在这个阶段之后,我们可以确定每个网络层中每个神经元的输出信号值。下图显示了信号如何通过网络传播,符号 (w_{(xm)n}) 表示输入层网络输入 (x_m) 和神经元 (n) 之间的连接的权重。符号 (y_n) 表示神经元 (n) 的输出信号。
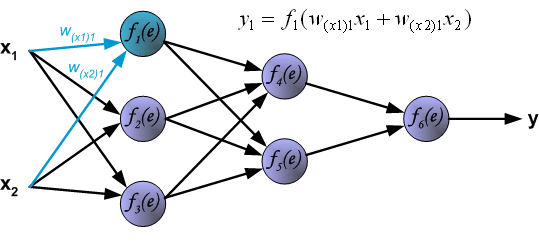
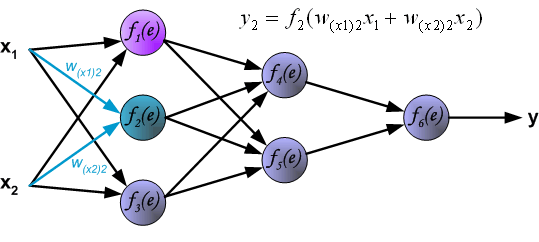
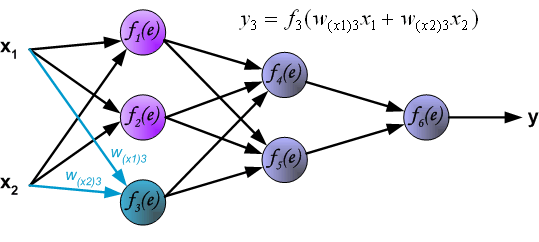
通过隐藏层传播信号。符号 (w_{(xm)n}) 表示神经元m的输出和下一层神经元 (n) 的输入之间的连接的权重。
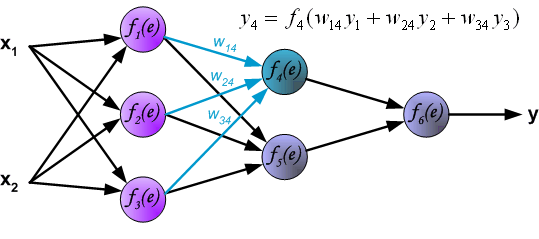
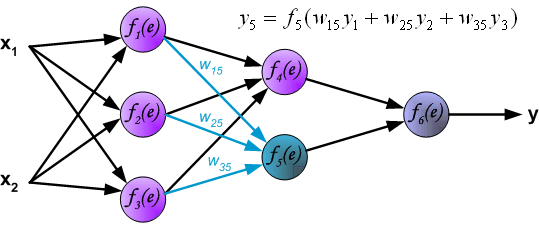
通过输出层传播信号。
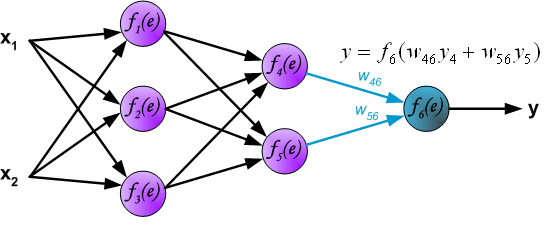
在下一个算法步骤中,将网络 (y) 的输出信号与在训练数据集中找到的所需输出值(目标)进行比较。差异称为输出层神经元的误差信号 (δ) 。
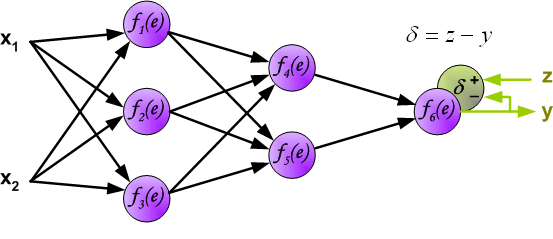
因为中间层神经元的输出值是未知的,所以不可能直接计算中间层神经元的误差。一直以来都没找到有效的方式训练多层神经网络。直到八十年代中期,反向传播算法才被提出。这个想法是将误差信号 (δ) (在每次训练中计算)传播回所有神经元,输出信号又被输入到之前的神经元。
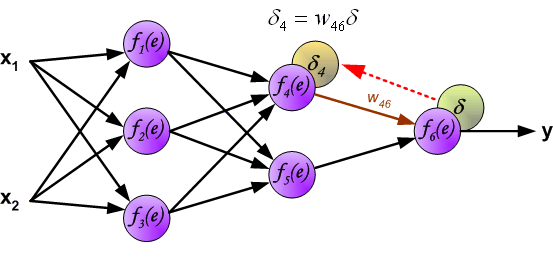
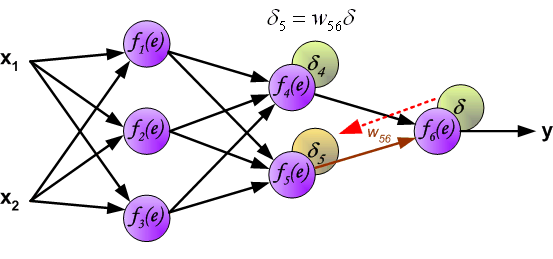
在反向传播过程中(信号从输出到输入一个接一个地传播)。中间层神经元的误差信号等于所有它输出指向的下一层神经元的误差和。用于累加误差的权重系数 (w_{(xm)n}) 等于计算输出值时使用的权重系数。如下图:
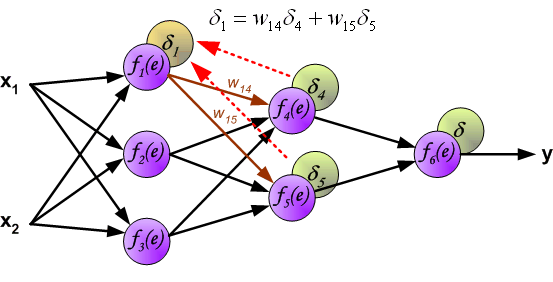
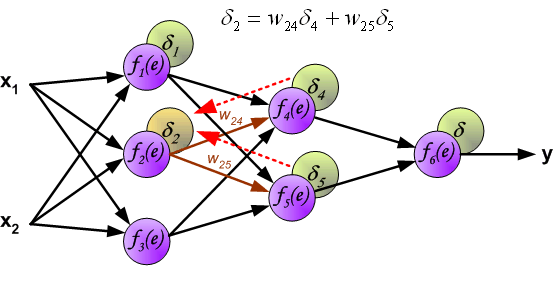
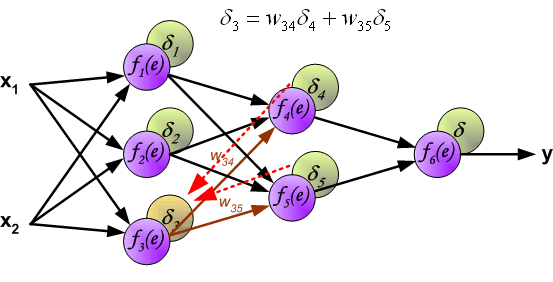
最终每个神经元输入节点的权重系数将被修改。在下面的公式中, (frac{d f(e)}{d e}) 表示当前计算新权重系数神经元激活函数的导数。
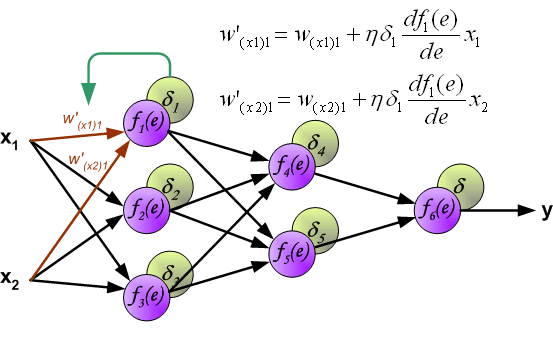
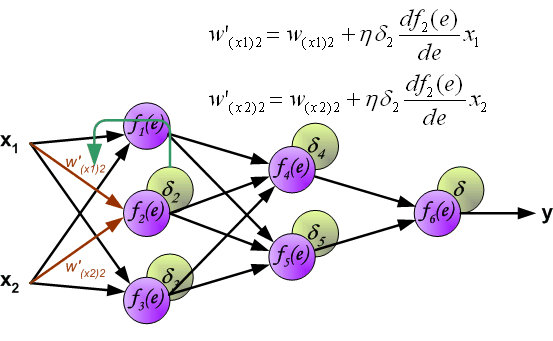
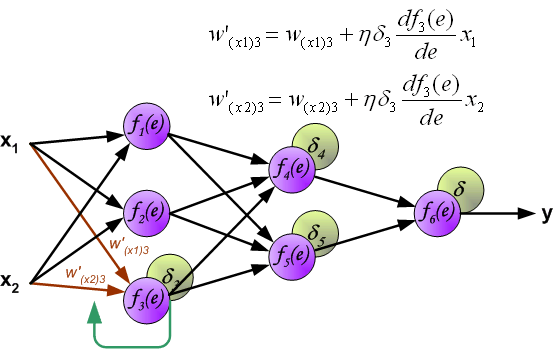
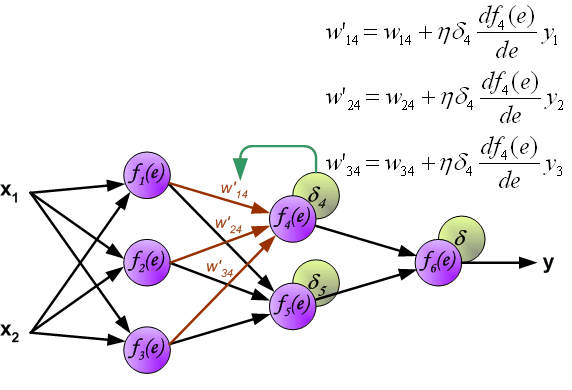
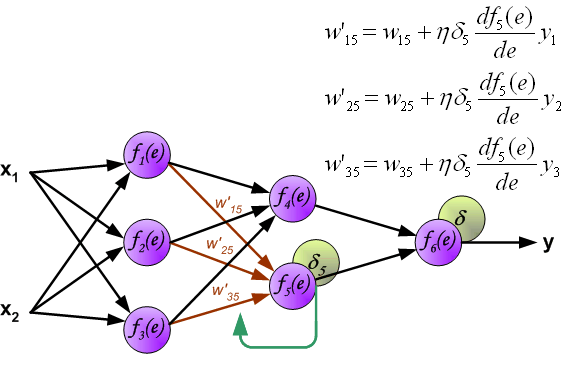
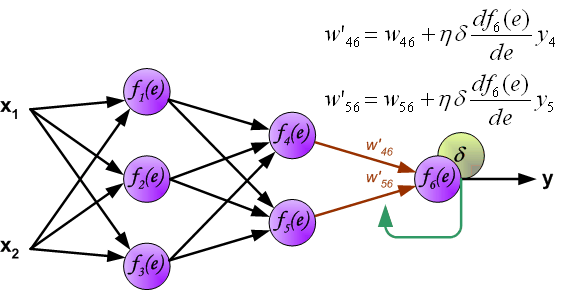
系数 (η) 影响网络训练速度。有几种方式来选择此系数 (η) 。第一种方法是在开始训练时设置较大的系数 (η) ,当权重系数不断修正时,系数 (η) 逐渐减少。第二个更复杂的方法是开始用小系数 (η) 进行训练。在训练过程中,当误差较大时系数 (η) 会增加,然后在最后阶段再次下降。在训练的开始具有较低的系数 (η) 可以确定权重系数的正负。