听完第四组的报告,我们小组对差分隐私的相关知识进行了搜索、学习和讨论,结合第四组的报告内容,有了一些新的认识和了解。接下来我们将针对差分隐私的思想做一个大致梳理。
- 为什么会产生差分隐私?
虽然已有的隐私保护方案层出不穷,但是它们有一个共同的缺点——都依赖攻击者的背景知识,没有对攻击模型做出合理假设。
而2006年Dwork等人提出的差分隐私模型解决了这个问题,差分隐私的概念来自于密码学中语义安全的概念,即攻击者无法区分出不同明文的加密结果。
由于有些“聪明”的用户为了知道某些信息,可以通过两次查询结果的差异进行对比,从而在两次数据的对比中找到有用的信息。正如在第四组的报告中提到的查询二等兵约瑟夫阿伦是否阵亡的信息,可以通过查询D5和D6两次数据结果,将两次数据结果进行对比就可以知道约瑟夫阿伦是否阵亡的消息。
- 差分隐私的主要思想:
差分隐私并不是要求保证数据集的整体性的隐私, 而是对数据集中的每个个体的隐私提供保护。它的概念要求每一个单一元素在数据集中对输出的影响都是有限的,即攻击者无法得知某一个个体是否存在于这样的一个数据集中。
为了达到保护隐私的目的,就必须使得数据集的计算处理结果对于具体某个记录的变化是不敏感的,单个记录在数据集中或不在数据集中,对计算结果的影响微乎其微,攻击者或其他恶意用户无法通过观察结果获取准确的个体信息。
应用例子:
数据如表1所示,其中的每个记录表示某个学生测试是否及格(1表示及格,0表示不及格)。
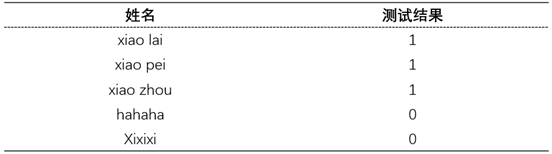
表 1 学生测试情况数据集
我们把表1中前3条记录当做数据集D1,前4条当做数据集D2。隐私算法A=count(i)+噪音,其中i=1,2,3.....
正常情况下:count(4)=3;(前四条记录,即数据集D1)
count(5)=3;(前五条记录,即数据集D2)
这样我们就可以推断第5条记录的值一定是0,会发生隐私泄露。
差分隐私保护情况下:count(4)+噪音与count(5)+噪音其结果均以几乎完全相同的概率输出{2,2,3,4}(这个结果只是假设)中的任意一个。其中几乎完全相同的概率:两者的概率差为。
- 那么如何实现差分隐私呢?
噪声机制是实现差分隐私保护的主要方法。拉普拉斯机制和指数机制是最常用的两种噪声机制。其中,拉普拉斯机制面向连续型数据的查询,而指数机制面向离散型数据的查询。上述两种噪声机制均与查询函数的全局敏感性密切相关,而全局敏感性则是定义在至多相差一条记录的近邻数据集之上,使得攻击者无法根据统计结果推测个体记录,即将个体记录隐藏在统计结果之中。
可以通过在查询结果上加入噪声来实现对用户隐私信息的保护,而噪声量的大小是一个关键的量,要使加入的噪声既能保护用户隐私,又不能使数据因为加入过多的噪声而导致数据不可用。函数敏感度是控制噪声的重要参数。Dwork等人在2006年,提出了全局敏感度以及拉普拉斯机制的概念,通过全局敏感度来控制生成的噪声大小,可以实现满足差分隐私要求的隐私保护机制。
总的来说,差分隐私是针对统计数据库的隐私泄露问题提出的一种新的隐私定义。使用差分隐私的条件比较苛刻,从上面的介绍中可以看到在加噪音的时候需要使用与原数据分布比较类似的噪音函数,而这一条件就限制了大多数数据其实不满足查分隐私的使用条件。