并查集
基本概念
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。
实现原理
通过更新维护父亲节点使得,合并后的集合最终拥有同一个点根节点,拥有相同根节点即为同类。
- Search 查找自己的根节点;(红圈标记为根节点)
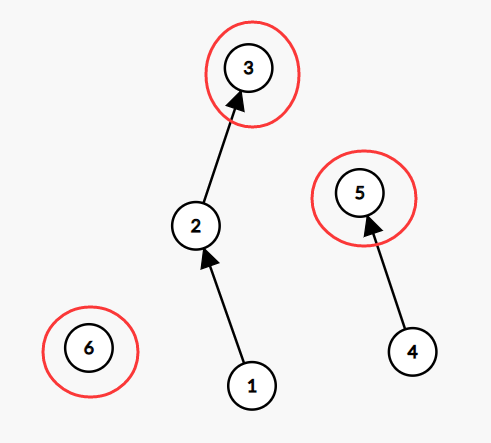
- Merge 合并两个节点在一个集合;(假设寻找合并节点5和2)
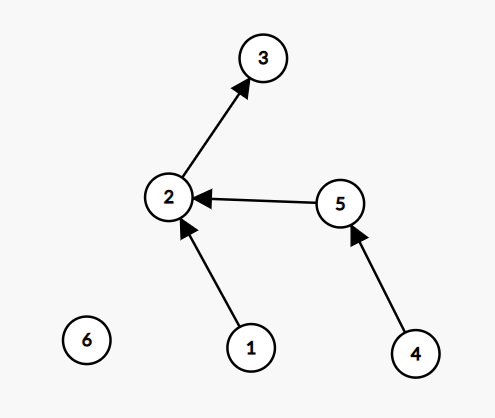
- 压缩路径;压缩路径可以使得在多次查询时,查询时间得到优化,具体过程是优化其结构,使得查询点的父亲节点为根节点。(上图压缩路径后得到)
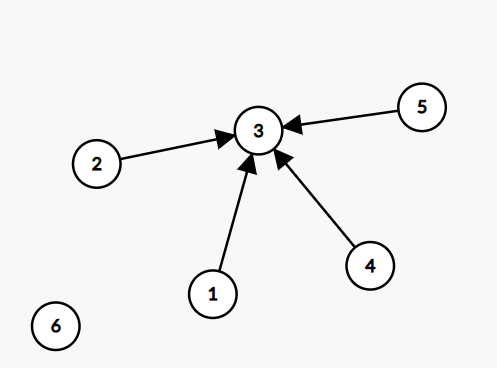
代码实现

1 void init(){ // 初始化自己祖先就是自己 2 for(int i = 1 ; i<= n; i++){ 3 pre[i] = i; 4 } 5 } 6 7 int Search(int x){ // 递归寻找自己的祖先 8 return x == pre[x] ? x : pre[x] = Search(pre[x]); 9 } 10 11 void Merge(int x, int y){ // 合并两个节点 12 int fx = Search(x); 13 int fy = Search(y); 14 if(fx != fy) pre[fx] = fy; // 把x合并到y即把x祖先设置为y的祖先 15 }
带权并查集
基本概念
带权并查集即是结点存有权值信息的并查集;当两个元素之间的关系可以量化,并且关系可以合并时,可以使用带权并查集来维护元素之间的关系;带权并查集每个元素的权通常描述其与并查集中祖先的关系,这种关系如何合并,路径压缩时就如何压缩;带权并查集可以推算集合内点的关系,而一般并查集只能判断属于某个集合。
经典例题
食物链(FJUTOJ2022 & POJ1182)
传送门:FJUTOJ2022 && POJ1182
题意:
动物王国中有三类动物A,B,C,A吃B, B吃C,C吃A。
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
用两种说法对这N个动物所构成的食物链关系进行描述:
- "1 X Y",表示X和Y是同类。
- "2 X Y",表示X吃Y。
给出K句话,有些是真的,有些是假的,满足下列任一条件即为假话,否则是真话:
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
输出假话的数量;
解题思路:
这个题目需要维护推算集合内部的关系,所以可以利用带权并查集解决。
创建利用pre数组和rela数组判断集合关系,pre判断集合之间的关系,rela判断集合内部元素的关系,这题我们可以建立三种关系同类,捕食,和被捕食三种关系,我们在rela数组中分别用0,1,2表示:
- 0表示和根节点是同类关系
- 1表示和跟节点是捕食关系(吃根节点)
- 2表示和根节点是被捕食关系(被根节点吃)
确定表示了三种关系表示,剩下是需要维护的关系,我们需要维护些什么关系呢?
首先是合并考虑压缩路径时的关系维护,我们压缩路径时已知B和A的关系,以及A和A根节点的关系,需要推导出B和A根节点的关系,如图是我们橙色线是我们要推导出的关系,黑色线是以知关系。
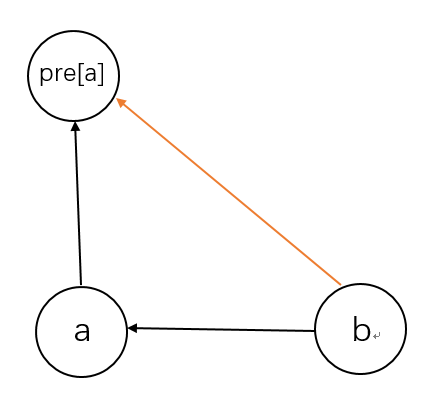
我们列举所有情况在表格中来看,是否存在某种关系。
| 结点B与A关系 | B与根关系 | |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 2 | 2 |
| 1 | 0 | 1 |
| 1 | 1 | 2 |
| 1 | 2 | 0 |
| 2 | 0 | 2 |
| 2 | 1 | 0 |
| 2 | 2 | 1 |
从表格中我们显然可以得到关系` rela[b] = (rela[a] + rela[b]) % 3`压缩路径关系的代码如下。

1 int Find(int x){ // 查找当前结点的根节点 2 if(x == pre[x]) return x; 3 else{ // 压缩路径 4 int temp = pre[x]; 5 pre[x] = Find(pre[x]); // 递归寻找头根点,压缩路径节点 6 rela[x] = (rela[x] + rela[temp]) % 3; // 压缩路径关系 7 } 8 return pre[x]; 9 }
然后我们考虑关系的查找,我们以及知道A和B在同一集合,即代表他们根节点相同,我们要确定两者之间的关系,我们还是线画出关系图,橙色线是我们要推导出的关系,黑色线是以知关系。
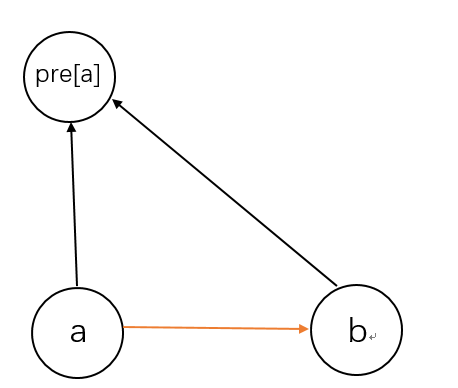
我们同样在表格中写出对应关系
从表格中可以得到关系`relation[a->b] = (rela[a] - rela[b]) % 3`,减法可能会产生负数,所以要先+3再进行取模,查找关系的代码如下

1 if(Find(x) == Find(y)){ // 如果两个根节点相同 2 relation = (rela[x] - rela[y] + 3) % 3; // 推出两个根节点之间的关系 3 return relation == r; // 判断给出关系是否与已经存在的关系矛盾 4 }
| 结点B与根关系 | A与B关系 | |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 2 |
| 0 | 2 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 2 | 2 |
| 2 | 0 | 2 |
| 2 | 1 | 1 |
| 2 | 2 | 0 |
最后我们考虑合并两个节点时关系的维护,我们已经知a和其根节点的关系,以及b和其根节点的关系,当我们把b集合合并到a集合时,我们需要考虑b根节点和a根节点存在的关系,关系图如下,橙色线是我们要推导出的关系,黑色线是以知关系。
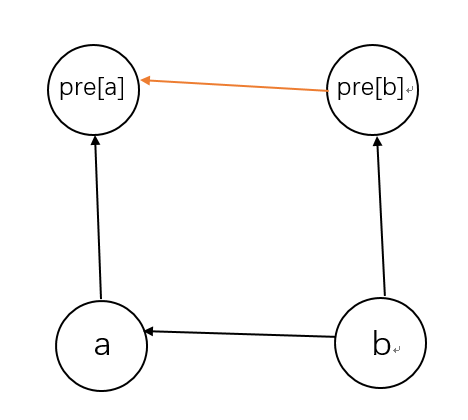
关系表如下
| 结点B与根关系 | 结点B与A的关系 | B根节点和A根节点的关系 | |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 2 | 2 |
| 0 | 1 | 0 | 2 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 2 | 1 |
| 0 | 2 | 0 | 1 |
| 0 | 2 | 1 | 2 |
| 0 | 2 | 2 | 0 |
上面这个表并没有列出所有情况,但是我们已经可以从表格中可以得到关系`relation[pre[b]->prea[a]] = (rela[a] - rela[b] + relation[b -> a]) % 3`合并关系的代码如下

1 void Merge(int x, int y, int r){ // 合并两个节点关系 2 int fx = Find(x); // 查找 x,y的根节点 3 int fy = Find(y); 4 5 if(fx != fy){ //如根节点不同进行合并 6 pre[fx] = fy; //把x节点集合合并到y 7 rela[fx] = (rela[y] - rela[x] + r + 3) % 3; //计算x头节点与y头节点的关系 8 } 9 }
AC代码

1 #include <cstdio> 2 #include <cstring> 3 #include <cmath> 4 #include <cstdlib> 5 #include <ctime> 6 #include <cctype> 7 #include <cstring> 8 #include <cmath> 9 #include <iostream> 10 #include <sstream> 11 #include <string> 12 #include <list> 13 #include <vector> 14 #include <set> 15 #include <map> 16 #include <queue> 17 #include <stack> 18 #include <algorithm> 19 #include <functional> 20 #define pr pair<int,LL> 21 #define lowbit(x) (x&(-x)) 22 #define rep(i,a,n) for (int i=a;i<=n;i++) 23 #define per(i,a,n) for (int i=a;i>=n;i--) 24 #define mem(ar,num) memset(ar,num,sizeof(ar)) 25 #define debug(x) cout << #x << ": " << x << endl 26 using namespace std; 27 typedef long long LL; 28 typedef unsigned long long ULL; 29 const int prime = 999983; 30 const int INF = 0x7FFFFFFF; 31 const LL INFF =0x7FFFFFFFFFFFFFFF; 32 const double pi = acos(-1.0); 33 const double inf = 1e18; 34 const double eps = 1e-6; 35 const LL mod = 1e9 + 7; 36 const int maxn = 5e5 + 7; 37 const int maxm = 4e6 + 7; 38 39 40 inline int read () { //读入优化 41 int X = 0, w = 1; char ch = 0; 42 while(ch < '-') { if(ch == '-') w = -1; ch = getchar(); } 43 while(ch >= '0' && ch <= '9') X = (X << 3) + (X << 1) + ch - '0', ch = getchar(); 44 return X * w; 45 } 46 47 int pre[maxn],rela[maxn]; 48 int n, k, ans; 49 50 void init() // 初始化 51 { 52 for(int i = 1; i <= n; i++){ 53 pre[i] = i; // 头节点等于自己本身 54 rela[i] = 0; // 自己和自己肯定是同类 55 } 56 ans = 0; //记录假话数量 57 } 58 59 int Find(int x){ // 查找当前结点的根节点 60 if(x == pre[x]) return x; 61 else{ // 压缩路径 62 int temp = pre[x]; 63 pre[x] = Find(pre[x]); // 递归寻找根节点,压缩路径节点 64 rela[x] = (rela[x] + rela[temp]) % 3; // 压缩路径关系 65 } 66 return pre[x]; 67 } 68 69 void Merge(int x, int y, int r){ // 合并两个节点关系 70 int fx = Find(x); // 查找 x,y的根节点 71 int fy = Find(y); 72 73 if(fx != fy){ //如根节点不同进行合并 74 pre[fx] = fy; //把x节点集合合并到y 75 rela[fx] = (rela[y] - rela[x] + r + 3) % 3; //计算x头节点与y头节点的关系 76 } 77 78 } 79 80 bool solve(int x,int y,int r){ // 判断真话假话 81 int relation; 82 if(x > n||y > n||(r == 1&&x == y)){ // 根据题意直接判断的假话 83 return false; 84 } 85 if(Find(x) == Find(y)){ // 如果两个根节点相同 86 relation = (rela[x] - rela[y] + 3) % 3; // 推出两个根节点之间的关系 87 return relation == r; // 判断给出关系是否与已经存在的关系矛盾 88 } 89 else 90 return true; //否则为真 91 } 92 /// 0 表示与根节点是同类 93 /// 1 表示与根节点是捕食关系 94 /// 2 表示与根节点是被捕食关系 95 int main() 96 { 97 n = read(); 98 k = read(); 99 init(); 100 int c, x, y; 101 while(k--){ 102 c = read(); 103 x = read(); 104 y = read(); 105 c --; 106 if(solve(x,y,c)){ 107 Merge(x,y,c); //真话合并两个节点关系 108 }else{ 109 ans++; //假话答案自增 110 } 111 } 112 printf("%d ",ans); 113 return 0; 114 }
我在刚学习带权并查集时看的是这位大佬的博客,大家也可以进行参考:带权并查集
第一次写博客,以上是我的一些个人理解,如有错误麻烦各位大佬指正。
