打印数组的所有子集
作者:Grey
原文地址:
无重复值情况
题目描述见: LeetCode 78. Subsets
主要思路
定义递归函数
void p(int[] arr, int i, LinkedList<Integer> pre, List<List<Integer>> result)
递归含义是:数组arr从i往后开始收集所有的子集,i之前生成的子集是pre,所有生成的子集都存在result中,
base case 就是,当i来到arr.length位置的时候,此时,已经没有选的字符了,将收集到的pre加入result中,
针对普遍情况,可能性有两种,第一种,不要选择i位置的元素,那么接下来直接调用p(arr, i + 1, pre, result)
第二种情况,选择i位置的元素,则将i位置的元素加入pre的下一个位置中,即:pre.addLast(arr[i]),然后去下一个位置做决策,即p(arr, i + 1, pre, result)。
第二种情况中,不要忘记选择了i位置的元素,在后续决策完毕后,需要恢复现场,即pre.removeLast()。
完整代码见
class Solution {
public static List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
p(nums, 0, new LinkedList<>(), result);
return result;
}
// i往后收集所有的子集
public static void p(int[] arr, int i, LinkedList<Integer> pre, List<List<Integer>> result) {
if (i == arr.length) {
List<Integer> ans = new ArrayList<>(pre);
result.add(ans);
} else {
// 不要i位置
p(arr, i + 1, pre, result);
pre.addLast(arr[i]);
// 要i位置
p(arr, i + 1, pre, result);
// 恢复现场
pre.removeLast();
}
}
}
有重复值情况
题目描述见: LeetCode 90. Subsets II
上一个问题由于题目限定了,没有重复元素,所以处理相对简单一些,本题说明了输入参数中可能会有重复的元素,且生成的子集不能有重复,此时有两个思路:
第一个思路,基于上一个问题的结果,即result,做去重操作,思路比较简单,但是复杂度会相对高一些,因为我们每次都要全量得到所有的子集,然后最后才去重。
第二个思路,在执行递归函数的时候,可以做一些剪枝,无须到最后再来去重,直接在递归函数中就把结果生成出来。接下来讲第二个解法的思路。
由于题目中已经说明,返回子集的顺序无要求,那么,我们可以首先将数组进行排序,排序后,所有相同的元素一定会排列到一起,然后定义一个和上一题一样的递归函数
void p(int[] nums, int i, LinkedList<Integer> pre, List<List<Integer>> result)
递归含义是:数组arr从i往后开始收集所有的无重复子集,i之前生成的子集是pre,所有生成的子集都存在result中。
接下来分析递归函数的可能性,我们可以不要选择i位置的元素,那么则可以直接加入result.add(new ArrayList<>(pre)),按上一题逻辑,接下来我们应该去i+1位置收集结果,但是,由于有重复元素,所以接下来i,i+1,……i + n 都有可能是同一个元素,示例图如下
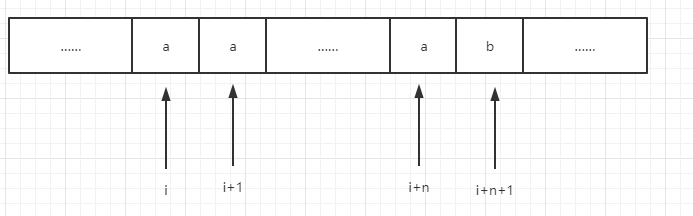
如上图,i一直到i+n都是元素a,直到i+n+1才是一个不同的元素,所以,当我们收集了i位置的元素以后,我们不能直接去i+1位置收集,而是应该从i+n+1位置开始收集。
完整代码见
class Solution {
public static List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> lists = new ArrayList<>();
Arrays.sort(nums);
p(nums, 0, new LinkedList<>(), lists);
return lists;
}
public static void p(int[] nums, int i, LinkedList<Integer> pre, List<List<Integer>> result) {
result.add(new ArrayList<>(pre));
for (int s = i; s < nums.length; s++) {
// 一直到下一个不等于s位置元素的地方
if (s > i && nums[s] == nums[s - 1]) {
continue;
}
pre.add(nums[s]);
p(nums, s + 1, pre, result);
pre.remove(pre.size() - 1);
}
}
}