A:水题,直接暴搜就好了。
1 class Solution { 2 public: 3 int res; 4 void dfs(vector<int>&nums,int i,int sum){ 5 if(i==nums.size()){ 6 res+=sum; 7 return ; 8 } 9 dfs(nums,i+1,sum); 10 dfs(nums,i+1,sum^nums[i]); 11 } 12 int subsetXORSum(vector<int>& nums) { 13 dfs(nums,0,0); 14 return res; 15 } 16 };
B:给定一个01串,问经过多少次操作能够将其变成交错串。(操作一次可将任意两个字符交换)如果不能返回 -1.
可以发现最终的答案,也就是交错串无非是两种,1打头和0打头。取二者min即可。
那么如何计算源串到目标串需要的操作次数呢?(目标串已知)
源串和目标串的区别无非就是两种01,和10(01表示某个位置源串是0,目标串是1),01数目记为 x ,10数目记为 y 。
而一次操作交换的双方只有可能四种情况 0 0 ,0 1 ,1 0 ,1 1
接下来以 交换0 1举例,源串.....0.....1...... 源串.......0.......0......
目标串...1.......0..... 目标串......1.......1......
交换源串0 1 后x -=1 ,y-=1,而交换0 0 后x ,y 不变。
所以如果x==y,那么操作次数也就等于x或者y,否则返回-1(因为x!=y就没有办法将其二者同时减到0)
1 class Solution { 2 public: 3 int get(string s1,string s2){ 4 int x=0,y=0; 5 int n=s1.size(); 6 for(int i=0;i<n;i++){ 7 if(s1[i]!=s2[i]){ 8 if(s1[i]=='0') x++; 9 else y++; 10 } 11 } 12 if(x!=y) return INT_MAX; 13 return x; 14 } 15 int minSwaps(string s) { 16 int n=s.size(); 17 string a(n,'1'),b(n,'1'); 18 for(int i=0;i<n;i+=2) a[i]='0'; 19 for(int i=1;i<n;i+=2) b[i]='0'; 20 int res=min(get(s,a),get(s,b)); 21 if(res==INT_MAX) 22 return -1; 23 return res; 24 } 25 };
C:题目如图

nums1.size()<=1000 , nums2.size()<=1e5
我们可以枚举nums1,现在只需要解决掉如何快速从nums2中查出对于nums1[i]有多少个数可使得和为tot。
hash表。
1 typedef long long LL; 2 class FindSumPairs { 3 public: 4 unordered_map<LL,LL> cnt; 5 vector<int> nums1,nums2; 6 FindSumPairs(vector<int>& nums1, vector<int>& nums2) { 7 this->nums1=nums1; 8 this->nums2=nums2; 9 for(int i=0;i<nums2.size();i++){ 10 cnt[nums2[i]]++; 11 } 12 } 13 14 void add(int index, int val) { 15 cnt[nums2[index]]--; 16 nums2[index]+=val; 17 cnt[nums2[index]]++; 18 } 19 20 int count(int tot) { 21 int res=0; 22 for(int i=0;i<nums1.size();i++){ 23 res+=cnt[tot-nums1[i]]; 24 } 25 return res; 26 } 27 }; 28 29 /** 30 * Your FindSumPairs object will be instantiated and called as such: 31 * FindSumPairs* obj = new FindSumPairs(nums1, nums2); 32 * obj->add(index,val); 33 * int param_2 = obj->count(tot); 34 */
D:经典斯特林数问题。
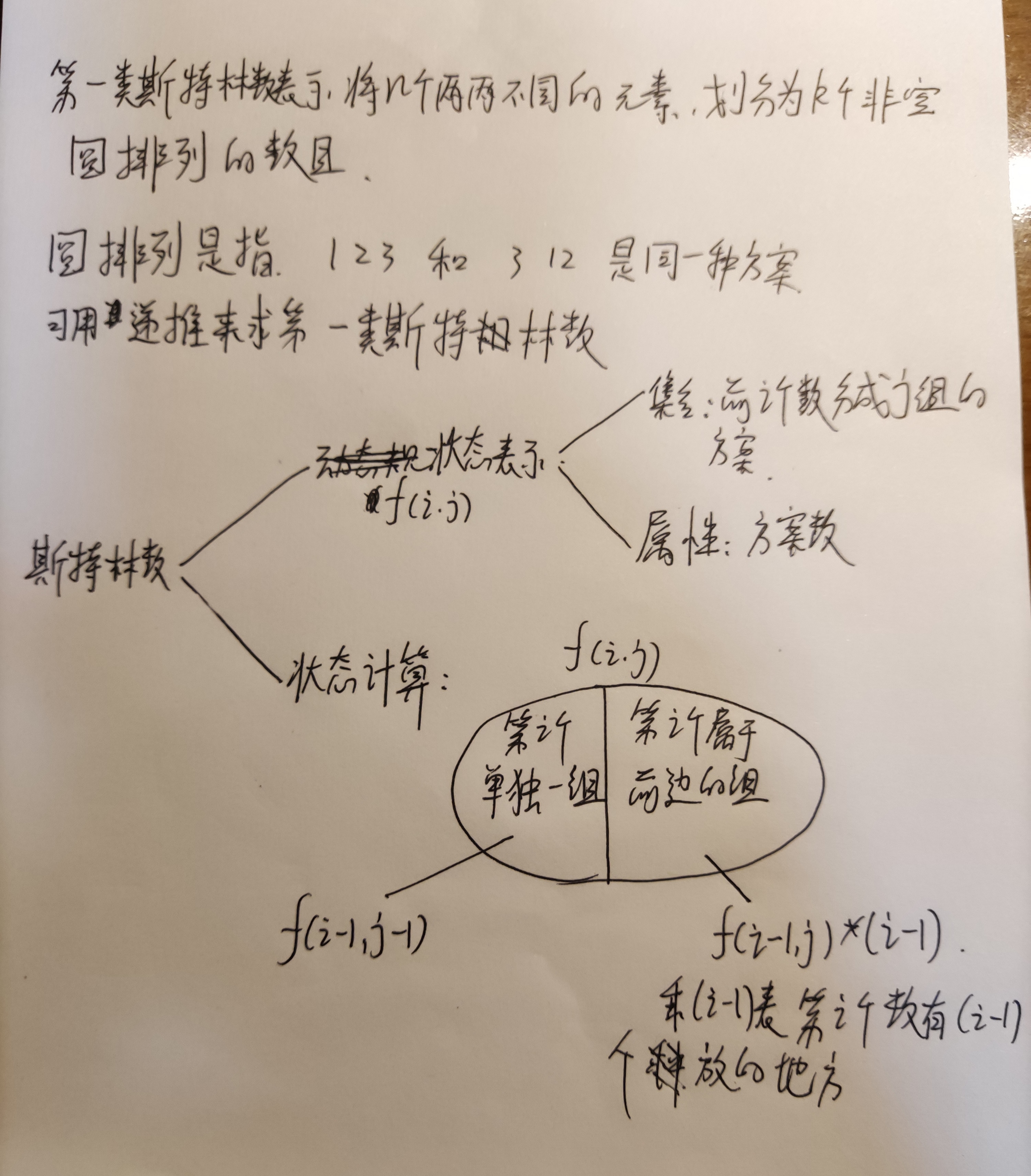
补充:圆排列可理解为固定一个元素之后,其余元素取全排列,也即A(n,n)/n
//将给定的集合分为k组,每一组中,固定一个元素,其余元素全排列 //也就没将每组的元素圆排列 //这是经典的第一类斯特林数的问题 const int N=1010,MOD=1e9+7; int f[N][N]; class Solution { public: int rearrangeSticks(int n, int k) { f[0][0]=1; for(int i=1;i<=n;i++){ for(int j=1;j<=k;j++){ f[i][j]=(f[i-1][j-1]+(long long)(i-1)*f[i-1][j])%MOD; } } return f[n][k]; } };