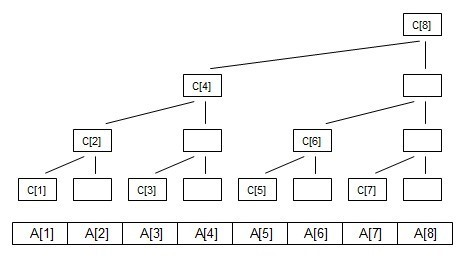
开局一张图,剩下全靠编。
对于树状数组,我的理解是有技巧的应用前缀和+神仙一般的二进制规律
1、改点求段
改点从下往上,将全部包括了这个点的c全部更改
1 int lowbit(int x) 2 { 3 return x&(-x); 4 }
1 void add(int x,int y)//将第x个数加上y 2 { 3 a[x]+=y; 4 for(int i=x;i<=n;i+=lowbit(i)) 5 { 6 c[i]+=y; 7 } 8 }
求段就是将大段分成一个一个的小段
1 int getsum(int x)//求[1,x]的和 2 { 3 int ans=0; 4 for(int i=x;i>0;i-=lowbit(i)) 5 { 6 ans+=c[i]; 7 } 8 return ans; 9 }
c数组的初始化就是在每一次输入a的时候在初始为0的a上add(i,a[i]);
2、改段求点
主要是用了差分的思想,然后用树状数组来维护差分数组
具体就是
改的话:在[x,y]区间内加上k,对差分数组的影响就只有d[x]和d[y+1],直接对这两个进行树状数组经典操作就好了
1 int d[N]; 2 int c[N]; 3 int n,m; 4 int lowbit(int x) 5 { 6 return x&(-x); 7 } 8 void add(int x,int y)//x位置加上y 9 { 10 d[x]+=y; 11 for(int i=x;i<=n;i+=lowbit(i)) 12 { 13 c[i]+=y; 14 } 15 } 16 void update(int x,int y,int k)//[x,y]区间内加上k 17 { 18 add(x,k); 19 add(y+1,-k); 20 }
查的话:因为a[i](原值)=d[1]+...+d[i],所以又是树状数组的经典getsum操作
1 int ask(int x)//查询a[i]直接d[1]...d[i]的和就是a[i] 2 { 3 int res=0; 4 for(int i=x;i>0;i-=lowbit(i)) 5 { 6 res+=c[i]; 7 } 8 return res; 9 }