博客作业06--图

1.学习总结

1.1图的思维导图

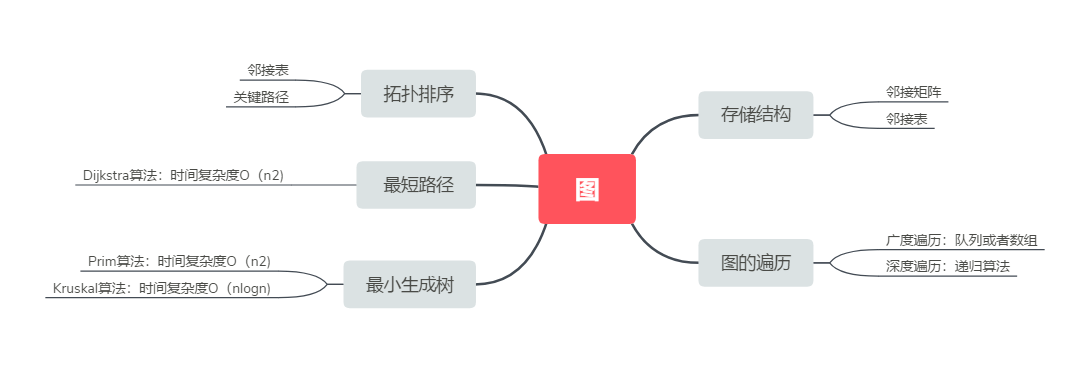
1.2 图结构学习体会

深度遍历算法:DFS,通过递归的算法来实现深度遍历。
广度遍历算法：BFS，通过队列的方式来实现广度遍历。
Prim和Kruscal算法：用来求最小生成树。
Dijkstra算法：用来求最短路径，通过path数组存放前驱，dist数组存放从初始点到下标点的权值。
拓扑序列：只有有向无环图才能用拓扑序列，可判断这个图是否有回路。

2.PTA实验作业

题目1：7-2 排座位

设计思路

   定义一个数组存储关系a[][]
   初始化都为0； 
   判断他们之间的关系
   if(a[i][j]=1) 即他们是朋友No problem
   if(a[i][j]=0) 即他们没有关系OK
   if(a[i][j]=-1) {
 	  如果有共同朋友则OK but...
	  如果没有朋友No way 
  } 

代码截图

PTA提交列表说明

一开始我设置的flag=1没有在一次操作后重新初始化，导致错误，因为根据所给例子我得出左后两个都是OK but...所以很容易找出错误。

题目2：7-3 六度空间

设计思路

  将初始点进队 
  last作为每一层的最后一个元素，level作为层数 ，vis[]来标记是否访问过
  while(队列不空时){
  	进行广度遍历
	  if(vis[]=0) count++//没有访问过
	  if(vis[]=1) //已被访问
	  当z=last时，表示这一层已被全部访问 level++,更新last
	  if(level=6) 退出循环
	  并且将count/n可得出关系百分比。 
 } 

代码截图

PTA提交列表说明

这一题在同学和老师的讲解后，做起来就比较顺手了。

题目3：7-4 公路村村通

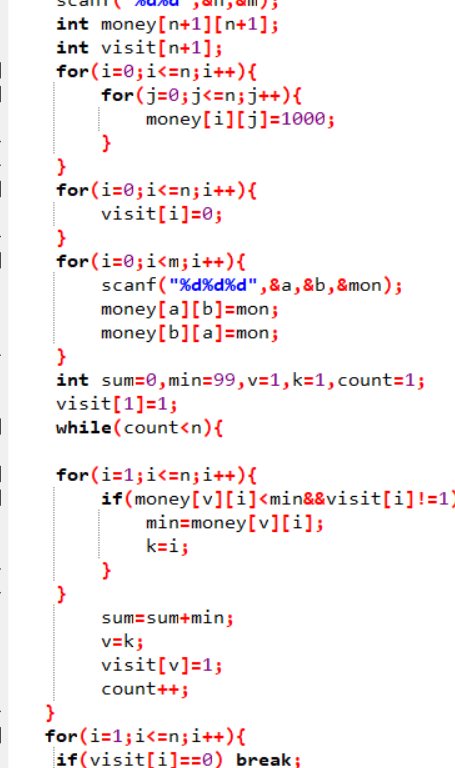
设计思路

定义visit[]来储存是否已经读取，money[][]储存权值，
sum记录总的需要数，count记录已经读取二点个数 
for(1 to n) 初始化将所有权值均设为1000
while(count < n){
	从v=1开始，找最短路径，通过visit[]判断路是否连接
	找到后visit[]=1，count++;sum+=money[v][i];
	 v=i;
} 

代码截图

PTA提交列表说明

我在做的过程中因为我只考虑了一条路接一条路例如1->2,然后从2开始重新找，其实可以1->2,1->3并不一定一条到黑，
我误用了贪心算法，最后从网上查阅了相关的信息，最终才过了。

3.截图本周题目集的PTA最后排名

我的总分：225

4. 阅读代码

城市紧急救援：https://blog.csdn.net/qq_26437925/article/details/47613719

#include <iostream>  
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <string>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>

using namespace std;

#define N 501
#define INF 99999999

int n, m, s, d;
int teams[N];
int mp[N][N];

bool vis[N];
int pre[N];
int amount[N];
int pathCount[N];
int dis[N];

void Dijkstra()
{
    int i;
    for (i = 0; i < n; i++)
    {
        pathCount[i] = 0;
        vis[i] = false;
        amount[i] = teams[i];
        pre[i] = -1;
        dis[i] = mp[s][i];
    }
    pathCount[s] = 1;
    dis[s] = 0;
    vis[s] = true;
    int newP = s;

    while (newP != d)
    {
        for (i = 0; i < n; i++)
        {
            if (!vis[i])
            {
                //
                if (dis[newP] + mp[newP][i] < dis[i])
                {
                    dis[i] = dis[newP] + mp[newP][i];
                    pathCount[i] = pathCount[newP];
                    amount[i] = amount[newP] + teams[i];
                    pre[i] = newP;
                }
                else if (dis[newP] + mp[newP][i] == dis[i])
                {
                    pathCount[i] += pathCount[newP];
                    if (amount[newP] + teams[i] > amount[i])
                    {
                        amount[i] = amount[newP] + teams[i];
                        pre[i] = newP;
                    }
                }
            }// if
        }// for

        int minn = INF;
        for (i = 0; i < n; i++)
        {
            if (!vis[i] && dis[i] < minn)
            {
                minn = dis[i];
                newP = i;
            }
        }
        vis[newP] = true;
    }// while
}

int main()
{
    //freopen("in", "r", stdin);
    while (scanf("%d%d%d%d", &n,&m,&s,&d) != EOF)
    {
        int i,j;
        for (i = 0; i < n; i++)
        {
            scanf("%d", &teams[i]);
        }
        for (i = 0; i < n; i++)
        {
            for (j = 0; j < n; j++)
            {
                mp[i][j] = INF;
            }
            mp[i][i] = 0;
        }
        int tmpi, tmpj,tmpdist;
        for (i = 0; i < m; i++)
        {
            scanf("%d%d%d", &tmpi, &tmpj, &tmpdist);
            mp[tmpi][tmpj] = tmpdist;
            mp[tmpj][tmpi] = tmpdist;
        }

        Dijkstra();

        printf("%d %d
", pathCount[d], amount[d]);

        vector<int> v;
        int lenv = 0;
        v.clear();
        int vn = d;
        while (vn != -1)
        {
            v.push_back(vn);
            lenv++;
            vn = pre[vn];
        }
        printf("%d", v[lenv-1]);
        for (i = lenv-2; i >= 0; i--)
        {
            printf(" %d", v[i]);
        }
        printf("
");
    }
    return 0;
}

根据dijkstra 算法来做这题，一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。
城市紧急救援就是按照最短路径问题来解决的。