一、如何分析一个排序算法
复杂度分析是整个算法学习的精髓。
-
时间复杂度: 一个算法执行所耗费的时间。
-
空间复杂度: 运行完一个程序所需内存的大小。
学习排序算法,我们除了学习它的算法原理、代码实现之外,更重要的是要学会如何评价、分析一个排序算法。分析一个排序算法,要从 执行效率、内存消耗、稳定性 三方面入手。
1、执行效率
1) 最好情况、最坏情况、平均情况时间复杂度
我们在分析排序算法的时间复杂度时,要分别给出最好情况、最坏情况、平均情况下的时间复杂度。除此之外,你还要说出最好、最坏时间复杂度对应的要排序的原始数据是什么样的。
2)时间复杂度的系数、常数 、低阶
我们知道,时间复杂度反应的是数据规模 n 很大的时候的一个增长趋势,所以它表示的时候会忽略系数、常数、低阶。但是实际的软件开发中,我们排序的可能是 10 个、100 个、1000 个这样规模很小的数据,所以,在对同一阶时间复杂度的排序算法性能对比的时候,我们就要把系数、常数、低阶也考虑进来。
3)比较次数和交换(或移动)次数
基于比较的排序算法的执行过程,会涉及两种操作,一种是元素比较大小,另一种是元素交换或移动。
所以,如果我们在分析排序算法的执行效率的时候,应该把比较次数和交换(或移动)次数也考虑进去。
2、内存消耗
也就是看空间复杂度。还需要知道如下术语:
-
内排序:所有排序操作都在内存中完成;
-
外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
-
原地排序:原地排序算法,就是特指空间复杂度是 O(1) 的排序算法。
3、稳定性
-
稳定:如果待排序的序列中存在值
相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。比如:a 原本在 b 前面,而 a = b,排序之后,a 仍然在 b 的前面; -
不稳定:如果待排序的序列中存在值
相等的元素,经过排序之后,相等元素之间原有的先后顺序改变。比如:a 原本在 b 的前面,而 a = b,排序之后, a 在 b 的后面;
二、冒泡排序
1、思想
-
冒泡排序只会操作相邻的两个数据。
-
每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。
-
一次冒泡会让至少一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作。
2、特点
-
优点:排序算法的基础,简单实用易于理解。
-
缺点:比较次数多,效率较低。
3、实现
// 冒泡排序(未优化)
const bubbleSort = arr => {
console.time('改进前冒泡排序耗时');
const length = arr.length;
if (length <= 1) return;
// i < length - 1 是因为外层只需要 length-1 次就排好了,第 length 次比较是多余的。
for (let i = 0; i < length - 1; i++) {
// j < length - i - 1 是因为内层的 length-i-1 到 length-1 的位置已经排好了,不需要再比较一次。
for (let j = 0; j < length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
const temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
console.log('改进前 arr :', arr);
console.timeEnd('改进前冒泡排序耗时');
};
优化:当某次冒泡操作已经没有数据交换时,说明已经达到完全有序,不用再继续执行后续的冒泡操作。
// 冒泡排序(已优化)
const bubbleSort2 = arr => {
console.time('改进后冒泡排序耗时');
const length = arr.length;
if (length <= 1) return;
// i < length - 1 是因为外层只需要 length-1 次就排好了,第 length 次比较是多余的。
for (let i = 0; i < length - 1; i++) {
let hasChange = false; // 提前退出冒泡循环的标志位
// j < length - i - 1 是因为内层的 length-i-1 到 length-1 的位置已经排好了,不需要再比较一次。
for (let j = 0; j < length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
const temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
hasChange = true; // 表示有数据交换
}
}
if (!hasChange) break; // 如果 false 说明所有元素已经到位,没有数据交换,提前退出
}
console.log('改进后 arr :', arr);
console.timeEnd('改进后冒泡排序耗时');
};
测试:

4、分析
-
第一,冒泡排序是原地排序算法吗 ?
冒泡的过程只涉及相邻数据的交换操作,只需要常量级的临时空间,所以它的空间复杂度为 O(1),是一个
原地排序算法。 -
第二,冒泡排序是稳定的排序算法吗 ?
在冒泡排序中,只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性,当有相邻的两个元素大小相等的时候,我们不做交换,相同大小的数据在排序前后不会改变顺序。所以冒泡排序是
稳定的排序算法。 -
第三,冒泡排序的时间复杂度是多少 ?
最佳情况:T(n) = O(n),当数据已经是正序时。
最差情况:T(n) = O(n2),当数据是反序时。
平均情况:T(n) = O(n2)。

三、插入排序
插入排序又为分为 直接插入排序 和优化后的 拆半插入排序 与 希尔排序,我们通常说的插入排序是指直接插入排序。
(一)直接插入排序
1、思想
一般人打扑克牌,整理牌的时候,都是按牌的大小(从小到大或者从大到小)整理牌的,那每摸一张新牌,就扫描自己的牌,把新牌插入到相应的位置。
插入排序的工作原理:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
2、步骤
-
从第一个元素开始,该元素可以认为已经被排序;
-
取出下一个元素,在已经排序的元素序列中从后向前扫描;
-
如果该元素(已排序)大于新元素,将该元素移到下一位置;
-
重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置;
-
将新元素插入到该位置后;
-
重复步骤 2 ~ 5。
3、实现
// 插入排序
const insertionSort = array => {
const len = array.length;
if (len <= 1) return
let preIndex, current;
for (let i = 1; i < len; i++) {
preIndex = i - 1; //待比较元素的下标
current = array[i]; //当前元素
while (preIndex >= 0 && array[preIndex] > current) {
//前置条件之一: 待比较元素比当前元素大
array[preIndex + 1] = array[preIndex]; //将待比较元素后移一位
preIndex--; //游标前移一位
}
if (preIndex + 1 != i) {
//避免同一个元素赋值给自身
array[preIndex + 1] = current; //将当前元素插入预留空位
console.log('array :', array);
}
}
return array;
};
测试
const array = [5, 4, 3, 2, 1];
console.log("原始 array :", array);
insertionSort(array);
// 原始 array: [5, 4, 3, 2, 1]
// array: [4, 5, 3, 2, 1]
// array: [3, 4, 5, 2, 1]
// array: [2, 3, 4, 5, 1]
// array: [1, 2, 3, 4, 5]
4、分析
-
第一,插入排序是原地排序算法吗 ?
插入排序算法的运行并不需要额外的存储空间,所以空间复杂度是 O(1),所以,这是一个
原地排序算法。 -
第二,插入排序是稳定的排序算法吗 ?
在插入排序中,对于值相同的元素,我们可以选择将后面出现的元素,插入到前面出现元素的后面,这样就可以保持原有的前后顺序不变,所以插入排序是
稳定的排序算法。 -
第三,插入排序的时间复杂度是多少 ?
最佳情况:T(n) = O(n),当数据已经是正序时。
最差情况:T(n) = O(n2),当数据是反序时。
平均情况:T(n) = O(n2)。
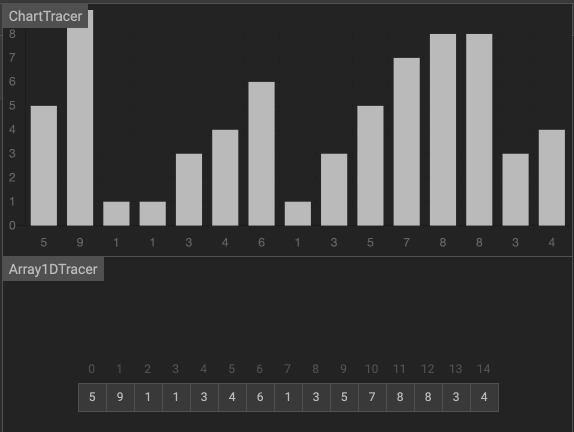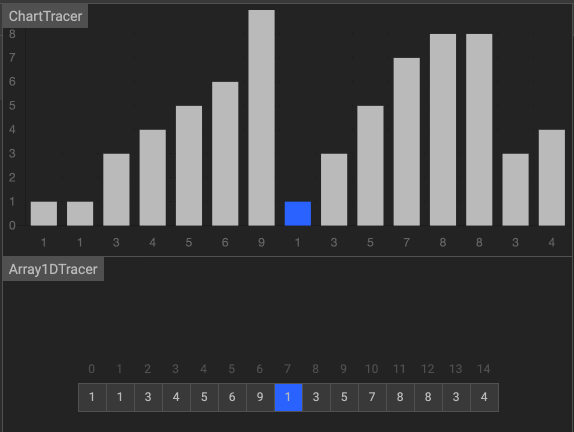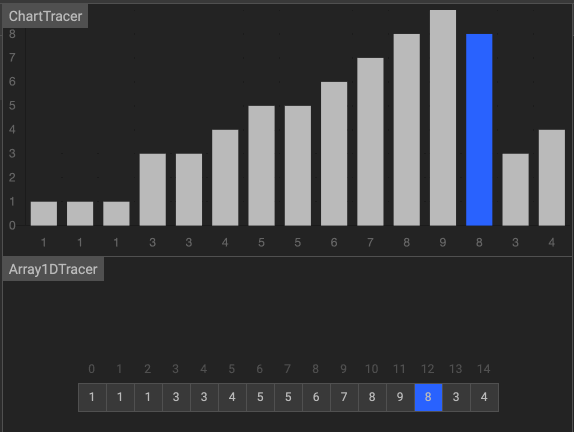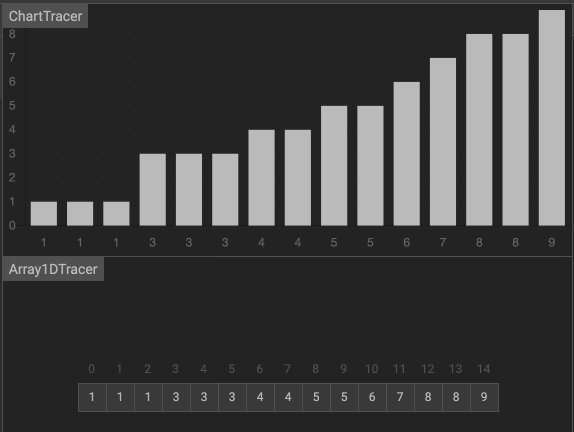
(二)拆半插入
插入排序也有一种优化算法,叫做拆半插入。
1、思想
折半插入排序是直接插入排序的升级版,鉴于插入排序第一部分为已排好序的数组,我们不必按顺序依次寻找插入点,只需比较它们的中间值与待插入元素的大小即可。
2、步骤
-
取 0 ~ i-1 的中间点 ( m = (i-1) >> 1 ),array[i] 与 array[m] 进行比较,若 array[i] < array[m],则说明待插入的元素 array[i] 应该处于数组的 0 ~ m 索引之间;反之,则说明它应该处于数组的 m ~ i-1 索引之间。
-
重复步骤 1,每次缩小一半的查找范围,直至找到插入的位置。
-
将数组中插入位置之后的元素全部后移一位。
-
在指定位置插入第 i 个元素。
注:x >> 1 是位运算中的右移运算,表示右移一位,等同于 x 除以 2 再取整,即 x >> 1 == Math.floor(x/2) 。
3、实现
// 折半插入排序
const binaryInsertionSort = array => {
const len = array.length;
if (len <= 1) return;
let current, i, j, low, high, m;
for (i = 1; i < len; i++) {
low = 0;
high = i - 1;
current = array[i];
while (low <= high) {
//步骤 1 & 2 : 折半查找
m = (low + high) >> 1; // 注: x>>1 是位运算中的右移运算, 表示右移一位, 等同于 x 除以 2 再取整, 即 x>>1 == Math.floor(x/2) .
if (array[i] >= array[m]) {
//值相同时, 切换到高半区,保证稳定性
low = m + 1; //插入点在高半区
} else {
high = m - 1; //插入点在低半区
}
}
for (j = i; j > low; j--) {
//步骤 3: 插入位置之后的元素全部后移一位
array[j] = array[j - 1];
console.log('array2 :', JSON.parse(JSON.stringify(array)));
}
array[low] = current; //步骤 4: 插入该元素
}
console.log('array2 :', JSON.parse(JSON.stringify(array)));
return array;
};
注意:和直接插入排序类似,折半插入排序每次交换的是相邻的且值为不同的元素,它并不会改变值相同的元素之间的顺序,因此它是稳定的。