
图
图是一种比较复杂的数据结构,不能说比较复杂,而是最复杂的。虽然接触到图的算法只有两道题,但是真的让我打开眼界,打开了深度优先和广度优先的大门。
- 岛屿数量
- 单词接龙
岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
方法:找出图中连成一片的1,就是岛屿
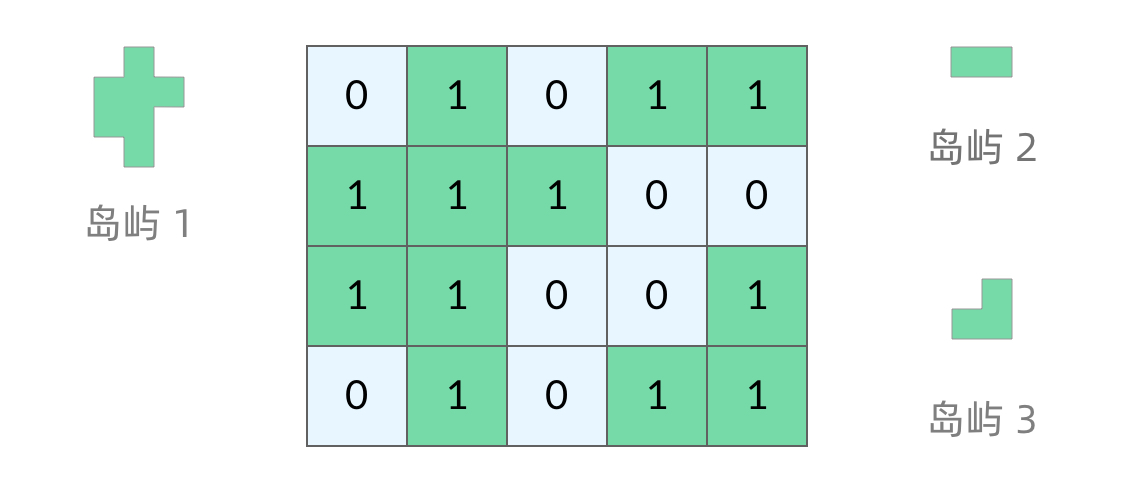
- 我们需要建立一个 visited 数组用来记录某个位置是否被访问过。
- 对于一个为 1 且未被访问过的位置,我们递归进入其上下左右位置上为 1 的数,将其 visited 变成 true。
- 重复上述过程
- 找完相邻区域后,我们将结果 res 自增1,然后我们在继续找下一个为 1 且未被访问过的位置,直至遍历完.
DFS

DFS是按照某一个方向,一直找到不满足条件为止。
先是 向上 一直到边界,然后向下到边界,再向左,最后向右。按照某一个方向一直到底
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
if not grid: return 0
count = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == '1':
self.dfs(grid, i, j)
count += 1
return count
# 深度优先算法。自己调用自己。
# 只有当这一片的1全部都被置0之后,才会退出,否则会调用下去。
def dfs(self, grid, i, j):
if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] != '1':
return
grid[i][j] = '0'
self.dfs(grid, i + 1, j)
self.dfs(grid, i - 1, j)
self.dfs(grid, i, j + 1)
self.dfs(grid, i, j - 1)
BFS

BFS 是搜索周边,一圈一圈扩大范围。以当前位置为中心,先判断上面是否符合条件,符合则加入队列中,在判断右边,加入队列,再oudo下面,最后左边。这样当前位置周围一圈都判断结束,同时队列中又保存有四个方向的数据,下一次循环四个方向分别再向外扩展。
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
count = 0
for row in range(len(grid)):
for col in range(len(grid[0])):
if grid[row][col] == '1': # 发现陆地
count += 1 # 结果加1
grid[row][col] = '0' # 将其转为 ‘0’ 代表已经访问过
# 对发现的陆地进行扩张即执行 BFS,将与其相邻的陆地都标记为已访问
# 下面还是经典的 BFS 模板
land_positions = collections.deque()
land_positions.append([row, col])
while len(land_positions) > 0:
x, y = land_positions.popleft()
for new_x, new_y in [[x, y + 1], [x, y - 1], [x + 1, y], [x - 1, y]]: # 进行四个方向的扩张
# 判断有效性
if 0 <= new_x < len(grid) and 0 <= new_y < len(grid[0]) and grid[new_x][new_y] == '1':
grid[new_x][new_y] = '0' # 因为可由 BFS 访问到,代表同属一块岛,将其置 ‘0’ 代表已访问过
land_positions.append([new_x, new_y])
return count
单词接龙
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
序列中第一个单词是 beginWord 。
序列中最后一个单词是 endWord 。
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典 wordList 中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出:0
解释:endWord "cog" 不在字典中,所以无法进行转换。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/word-ladder
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
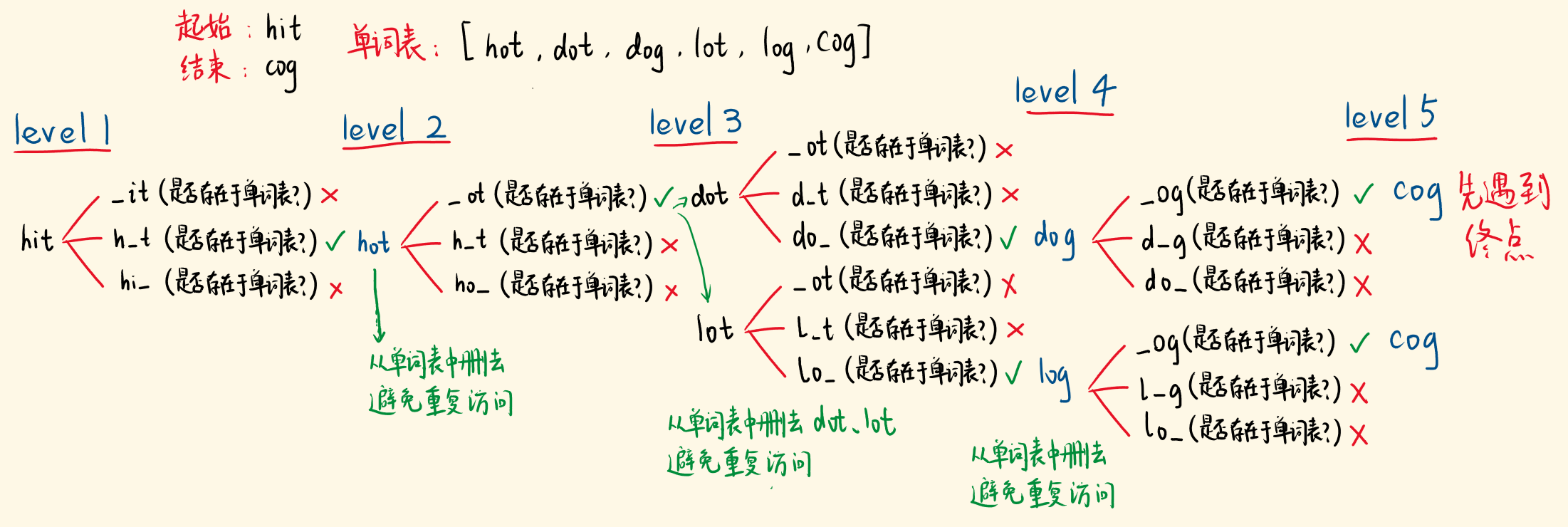
``思路`
从起点词出发,每次变一个字母,经过 n 次变换,变成终点词,希望 n 尽量小。
我们需要找出邻接关系,比如hit变一个字母会变成_it、h_t、hi_形式的新词,再看该新词是否存在于单词表,如果存在,就找到了一个下一层的转换词。
同时,要避免重复访问,hot->dot->hot这样变回来是没有意义的,徒增转换的长度。
所以,确定了下一个转换词,将它从单词表中删除(单词表的单词是唯一的)。
下一层的单词可能有多个,都要考察,哪一条转换路径先遇到终点词,它就最短。
整理一下
把单词看作节点,由一个结点带出下一层的邻接点,用BFS去做。
维护一个队列,让起点词入列,level 为 1,然后出列考察。
将它的每个字符变成26字母之一,逐个看是否在单词表,如果在,该新词为下一层的转变词。
将它入列,它的 level +1,并从单词表中删去这个词。
出列、入列…重复,当出列的单词和终点词相同,说明遇到了终点词,返回它的 level。
当队列为空时,代表BFS结束,始终没有遇到终点词,没有路径通往终点,返回 0。
作者:xiao_ben_zhu
链接:https://leetcode-cn.com/problems/word-ladder/solution/shou-hua-tu-jie-127-dan-ci-jie-long-bfsde-dian-x-2/
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
if not wordList and endWord not in wordList:
return 0
word_set = set(wordList)
if beginWord in word_set:
word_set.remove(beginWord)
from collections import deque
queue = deque()
queue.append([beginWord, 0])
while queue:
word, level = queue.popleft()
if word == endWord:
return level + 1
for i in range(len(word)):
for j in range(26):
new_word = word[:i] + chr(ord('a') + j) + word[i+1:]
if new_word in word_set:
word_set.remove(new_word)
queue.append([new_word, level+1])
return 0
# 图的小结
图虽然只有两道题,但是把深度优先和广度优先说的十分清楚。
深度优先: 循环 + 栈
广度优先: 循环 + 队列