平滑的目的也是正则化的目的之一,它是针对参数w而言,本质上就是要使得w的变化不要那么剧烈,有如下数学模型(假设最小化J):
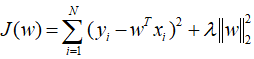
左侧是一个典型的线性回归模型,(xi,yi)就是实际的观测值,w就是估计的参数,右侧就是一个正则化项。可以直观的感受到,正则化项实际上起到了限制参数w的“变化程度或变化幅值”的作用,具体来说,它可以令w的任何一个分量相比较于剩余分量变化程度保持一致,不至于出现变化特别明显的分量。直接的作用就是防止模型“过拟合”,提高了模型的泛化性能。关于这一点,具体请见http://blog.csdn.net/wsj998689aa/article/details/39547771
拉普拉斯平滑应用在正则化上的时候,往往被称做“拉普拉斯惩罚”,惩罚的参数是w。
背景:机器学习中,大部分算法直接将图像(假设为M*N)按行或者列拉成向量,这样肯定会损失结构化信息。结构化信息是指,一个像素本来和它周围8个像素都有关系,你直接给拉成向量了,那么这种关系就直接被你给毁掉了,这就叫空间结构信息。这种信息属于先验信息,NFL定理说的很清楚:能够尽可能利用先验信息的学习算法才是好算法。看来,空间结构信息的破坏,会降低算法的”品味“。此时,拉普拉斯惩罚会帮助找回品味。一幅图像拉成向量x(M*N维),如果我们要通过拉普拉斯惩罚,补偿x上失去的结构信息。很简单,如下式: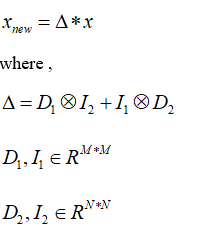
那个乘法是Kronecke积,相当于将乘号右边的每个元素替换成为左边矩阵数乘对应元素,如果A是一个 m x n 的矩阵,而B是一个 p x q 的矩阵,克罗内克积则是一个 mp x nq 的矩阵。
上述公式实际上起到的效果是,求一个矩阵中每个元素的水平方向和垂直方向的二阶差分之和,这个矩阵在这里可以被看错参数w的矩阵形式(按列reshape)。进一步,如果对一个线性回归模型加上拉普拉斯惩罚,模型就会变为如下形式:
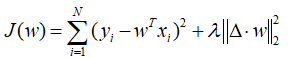
拉普拉斯惩罚使得模型更加平滑,比简单的2范数(岭回归)要好,因为它考虑了空间结构信息。常被用于PCA,LDA,LPP,NPE等子空间学习算法的改造上面,一般会使算法性能得到提升。
参考文献:Learning a Spatially Smooth Subspace for Face Recognition
原文:https://blog.csdn.net/wsj998689aa/article/details/40303561