uva 10755

http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1696

10755 - Garbage Heap

Time limit: 3.000 seconds

 

Garbage Heap

Time limit: 3.000 seconds

Memory limit: 64 megabytes

　　Farmer John has a heap of garbage formed in a rectangular parallelepiped.

　　It consists of a x b x c  garbage pieces each of which has a value. The value of a piece may be 0, if the piece is neither profitable nor harmful, and may be negative which means that the piece is not just unprofitable, but even harmful (for environment).

 

 

 

 

 

　　The farmer thinks that he has too much harmful garbage, so he wants to decrease the heap size, leaving a rectangular nonempty parallelepiped of smaller size cut of the original heap to maximize the sum of the values of the garbage pieces in it. You have to find the optimal parallelepiped value. (Actually, if any smaller parallelepiped has value less than the original one, the farmer will leave the original parallelepiped).

Input

　　     The first line of the input contains the number of the test cases, which is at most 15. The descriptions of the test cases follow. The first line of a test case description contains three integers A, B, and C (1 ≤ A, B, C ≤ 20). The next lines contain  a .b .c numbers, which are the values of garbage pieces. Each number does not exceed 2 ^ 31by absolute value. If we introduce coordinates in the parallelepiped such that the cell in one corner is (1,1,1) and the cell in the opposite corner is (A,B,C), then the values are listed in the order

 

 

 

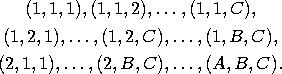
　　The test cases are separated by blank lines.

Output

　　　　For each test case in the input, output a single integer denoting the maximal value of the new garbage heap. Print a blank line between test cases.

Examples

Input	Output
1 2 2 2-1 2 0 -3 -2 -1 1 5	6

 

 

 

 

 

 

AC代码：

// UVa10755 Garbage heap

#include<cstdio>

#include<cstring>

#include<algorithm>

#define FOR(i,s,t)  for(int i = (s); i <= (t); ++i)

using namespace std;

 

void expand(int i, int& b0, int& b1, int& b2) {

  b0 = i&1; i >>= 1;

  b1 = i&1; i >>= 1;

  b2 = i&1;

}

 

int sign(int b0, int b1, int b2) {

  return (b0 + b1 + b2) % 2 == 1 ? 1 : -1;

}

 

const int maxn = 30;

const long long INF = 1LL << 60;

 

long long S[maxn][maxn][maxn];

 

long long sum(int x1, int x2, int y1, int y2, int z1, int z2) {

  int dx = x2-x1+1, dy = y2-y1+1, dz = z2-z1+1;

  long long s = 0;

  for(int i = 0; i < 8; i++) {

    int b0, b1, b2;

    expand(i, b0, b1, b2);

    s -= S[x2-b0*dx][y2-b1*dy][z2-b2*dz] * sign(b0, b1, b2);

  }

  return s;

}

 

int main() {

  int T;

  scanf("%d", &T);

  while(T--) {

    int a, b, c, b0, b1, b2;

    scanf("%d%d%d", &a, &b, &c);

    memset(S, 0, sizeof(S));

    FOR(x,1,a) FOR(y,1,b) FOR(z,1,c) scanf("%lld", &S[x][y][z]);

    FOR(x,1,a) FOR(y,1,b) FOR(z,1,c) FOR(i,1,7){

      expand(i, b0, b1, b2);

      S[x][y][z] += S[x-b0][y-b1][z-b2] * sign(b0, b1, b2);

    }

    long long ans = -INF;

    FOR(x1,1,a) FOR(x2,x1,a) FOR(y1,1,b) FOR(y2,y1,b) {

      long long M = 0;

      FOR(z,1,c) {

        long long s = sum(x1,x2,y1,y2,1,z);

        ans = max(ans, s - M);

        M = min(M, s);

      }

    }

    printf("%lld
", ans);

    if(T) printf("
");

  }

  return 0;

}