实验一 感知器及其应用

博客班级	班级连接
作业内容	作业连接
学号	3180701139
姓名	葛梦海

一、【实验目的】

1. 理解感知器算法原理，能实现感知器算法；

2. 掌握机器学习算法的度量指标；

3. 掌握最小二乘法进行参数估计基本原理；

4. 针对特定应用场景及数据，能构建感知器模型并进行预测。

二、【实验内容】

1. 安装Pycharm，注册学生版。

2. 安装常见的机器学习库，如Scipy、Numpy、Pandas、Matplotlib，sklearn等。

3. 编程实现感知器算法。

4. 熟悉iris数据集，并能使用感知器算法对该数据集构建模型并应用。

三、【实验报告要求]

1. 按实验内容撰写实验过程；

2. 报告中涉及到的代码，每一行需要有详细的注释；

3. 按自己的理解重新组织，禁止粘贴复制实验内容！

四、【实验过程及结果]

#导入包
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline

 # load data,下载数据
 iris = load_iris()
 df = pd.DataFrame(iris.data, columns=iris.feature_names)#生成表格
 df['label'] = iris.target

# 统计鸢尾花的种类与个数
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
df.label.value_counts() # value_counts() 函数可以对df里面label每个值进行计数并且排序，默认是降序

结果：
2 50
1 50
0 50
Name: label, dtype: int64

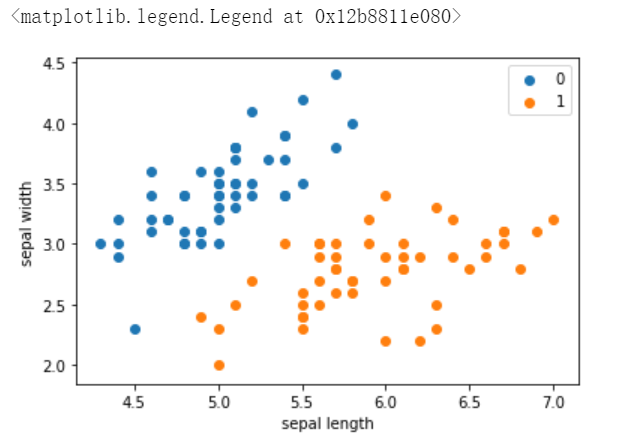
#画数据的散点图
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')#将数据的前50个数据绘制散点图
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')#将数据的50-100之间的数据绘制成散点图
plt.xlabel('sepal length')#给x坐标命名
plt.ylabel('sepal width')#给y坐标命名
plt.legend()

 #对数据进行预处理
 data = np.array(df.iloc[:100, [0, 1, -1]])#iloc函数：通过行号来取行数据,读取数据前100行的第0,1列和最后一列
 X, y = data[:,:-1], data[:,-1]#X为data数据中除去最后一列的数据，y为data数据的最后一列(y中有两类0和1)
 y = np.array([1 if i == 1 else -1 for i in y])#将y中的两类（0和1）改为（-1和1）两类

 # 定义算法
 # 此处为一元一次线性方程 
class Model:
    def __init__(self):
        self.w = np.ones(len(data[0])-1, dtype=np.float32) #初始w的值
        self.b = 0 #初始b的值为0
        self.l_rate = 0.1 #步长为0.1
        # self.data = data
 
    def sign(self, x, w, b):
        y = np.dot(x, w) + b #dot进行矩阵的乘法运算，y=w*x+b
        return y
 
    #随机梯度下降法
    def fit(self, X_train, y_train):
        is_wrong = False #初始假设有误分点
        while not is_wrong:
            wrong_count = 0 #误分点个数初始为0
            for d in range(len(X_train)):
                X = X_train[d] #取X_train一组及一行数据
                y = y_train[d] #取y_train一组及一行数据
                if y * self.sign(X, self.w, self.b) <= 0: #为误分点
                    self.w = self.w + self.l_rate*np.dot(y, X) #对w和b进行更新
                    self.b = self.b + self.l_rate*y
                    wrong_count += 1 #误分点个数加1
            if wrong_count == 0: #误分点个数为0，算法结束
                is_wrong = True
        return 'Perceptron Model!'
 
    def score(self):
        pass

 perceptron = Model()#生成一个算法对象
 perceptron.fit(X, y)#将测试数据代入算法中

结果：
'Perceptron Model!'

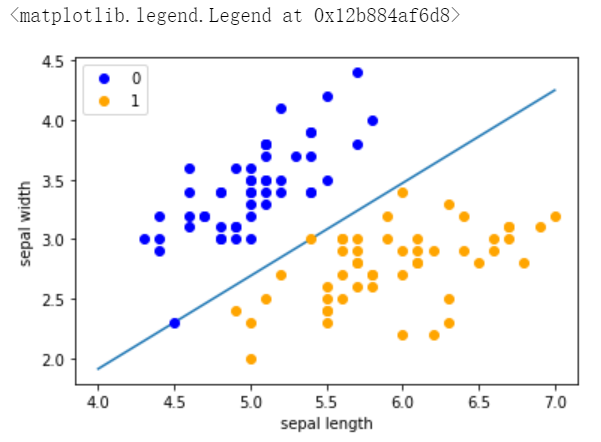
 #画出超平面
x_points = np.linspace(4, 7,10) #用于产生4,7之间的10点行矢量。其中4、7、10分别为起始值、中止值、元素个数。----产生x坐标
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1] #绘制超平面
plt.plot(x_points, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')#将数据的前50个数据绘制散点图
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')#将数据的50-100之间的数据绘制成散点图
plt.xlabel('sepal length')#给x坐标命名
plt.ylabel('sepal width')#给y坐标命名
plt.legend()

 #生成sklearn结果与上面手写函数的结果对比
from sklearn.linear_model import Perceptron ## 导入感知机模型
clf = Perceptron(fit_intercept=False, max_iter=1000, shuffle=False) 
#fit_intercept（默认True）是否对参数 b 进行估计，若为False则数据应是中心化的
#max_iter(默认1000）最大迭代次数
#shuffle（默认True）每轮训练后是否打乱数据
clf.fit(X, y)

结果：
Perceptron(alpha=0.0001, class_weight=None, early_stopping=False, eta0=1.0,
fit_intercept=False, max_iter=1000, n_iter_no_change=5, n_jobs=None,
penalty=None, random_state=0, shuffle=False, tol=0.001,
validation_fraction=0.1, verbose=0, warm_start=False)

 print(clf.coef_)#权值w参数
 print(clf.intercept_)#偏置b参数

结果：
[[ 16.3 -24.2]]
[0.]

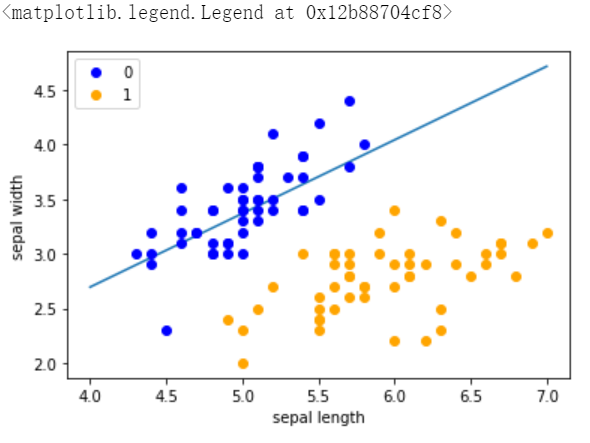
 #画出sklearn结果的散点图
x_ponits = np.arange(4, 8)#x,为4,5,6,7，默认步长为1，起始为4，终止为8，不取8
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]#绘制超平面
plt.plot(x_ponits, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')#将数据的前50个数据绘制散点图
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')#将数据的50-100之间的数据绘制成散点图
plt.xlabel('sepal length')#给x坐标命名
plt.ylabel('sepal width')#给y坐标命名
plt.legend()

五、【实验小结】
本次实验，安装了Pycharm学生版，并且学会了安装常见的机器学习库等。理解了感知器算法原理、并且能实现感知器算法。
感知器是人工神经网络中的一种典型结构， 它的主要的特点是结构简单。
它是一种二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别。
二分类模型
f(x)=sign(w∗x+b)
损失函数 L(w,b)=−Σyi(w∗xi+b)
算法
随即梯度下降法 Stochastic Gradient Descent随机抽取一个误分类点使其梯度下降。
w=w+ηyixi
b=b+ηyi
通过本次实验，我理解了感知器算法原理，能实现感知器算法；同时也掌握了机器学习算法的度量指标；
以及最小二乘法进行参数估计基本原理；对于一些特定应用场景及数据，能构建感知器模型并进行预测。