二项式分布

二项式分布

一个试验只有成功和失败两种可能性，这样的试验是伯努利试验。n个独立的伯努利试验中成功的次数的离散概率分布就是二项式分布。N次试验中正好得到k次成功的概率：
$$Binomleft( k|N,p ight) =(^{N}_{k})p^{k}left( 1-p ight) ^{N-k}$$
其中$(^{N}_{k})=dfrac {N!}{k!left( N-k ight) !}$，p是每次试验成功的概率。

---

二项式分布相关代码

#导入库
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

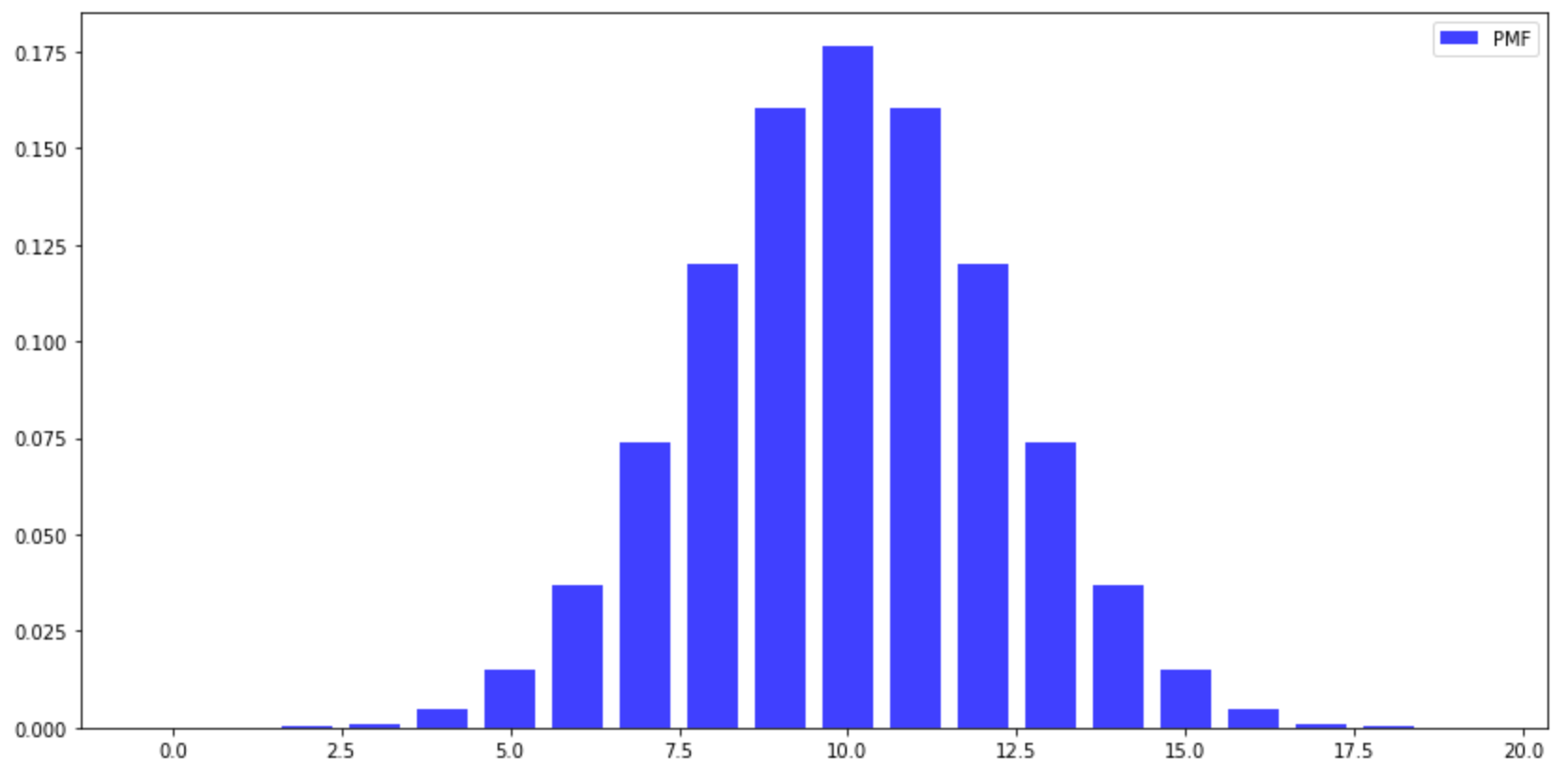
概率质量函数（PMF）

#PMF
#p=0.5,总共进行20次试验，成功k次试验的概率
plt.figure(figsize=(14,7))

plt.bar(np.arange(20),
        stats.binom.pmf(np.arange(20),p=0.5,n=20),
        width=0.75,
        alpha=0.75,
        color='b',
        label='PMF',
       )

plt.legend()
plt.show()

 

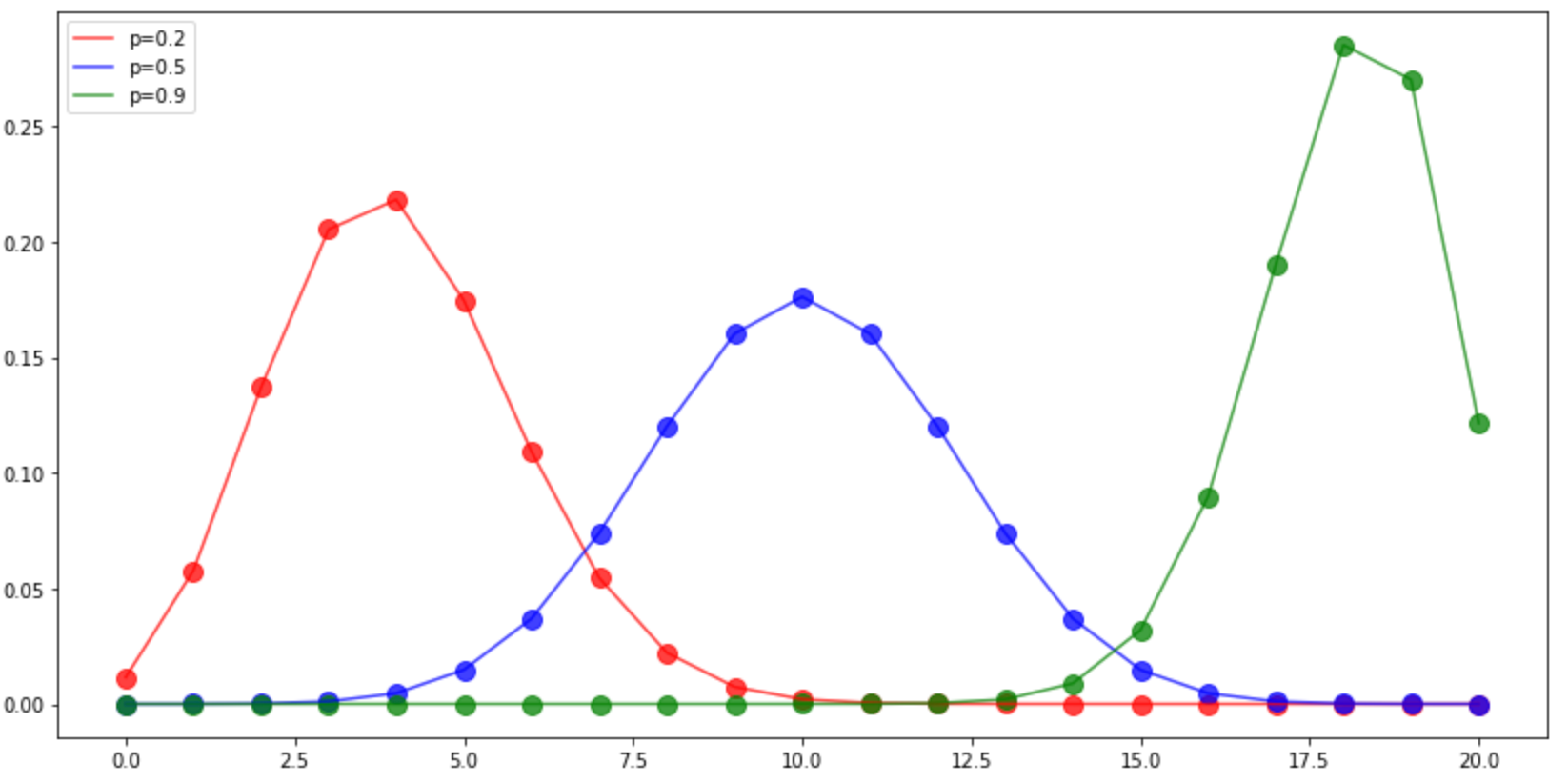
概率的影响

plt.figure(figsize=(14,7))

#p=0.2
plt.scatter(np.arange(21),
            stats.binom.pmf(np.arange(21),p=0.2,n=20),
            alpha=0.75,
            color='r',
            s=100,
           )
plt.plot(np.arange(21),
         stats.binom.pmf(np.arange(21),p=0.2,n=20),
         alpha=0.75,
         color='r',
         label='p=0.2',
        )

#p=0.5
plt.scatter(np.arange(21),
            stats.binom.pmf(np.arange(21),p=0.5,n=20),
            alpha=0.75,
            color='b',
            s=100,
           )
plt.plot(np.arange(21),
         stats.binom.pmf(np.arange(21),p=0.5,n=20),
         alpha=0.75,
         color='b',
         label='p=0.5',
        )

#p=0.9
plt.scatter(np.arange(21),
            stats.binom.pmf(np.arange(21),p=0.9,n=20),
            alpha=0.75,
            color='g',
            s=100,
           )
plt.plot(np.arange(21),
         stats.binom.pmf(np.arange(21),p=0.9,n=20),
         alpha=0.75,
         color='g',
         label='p=0.9',
        )

plt.legend()
plt.show()

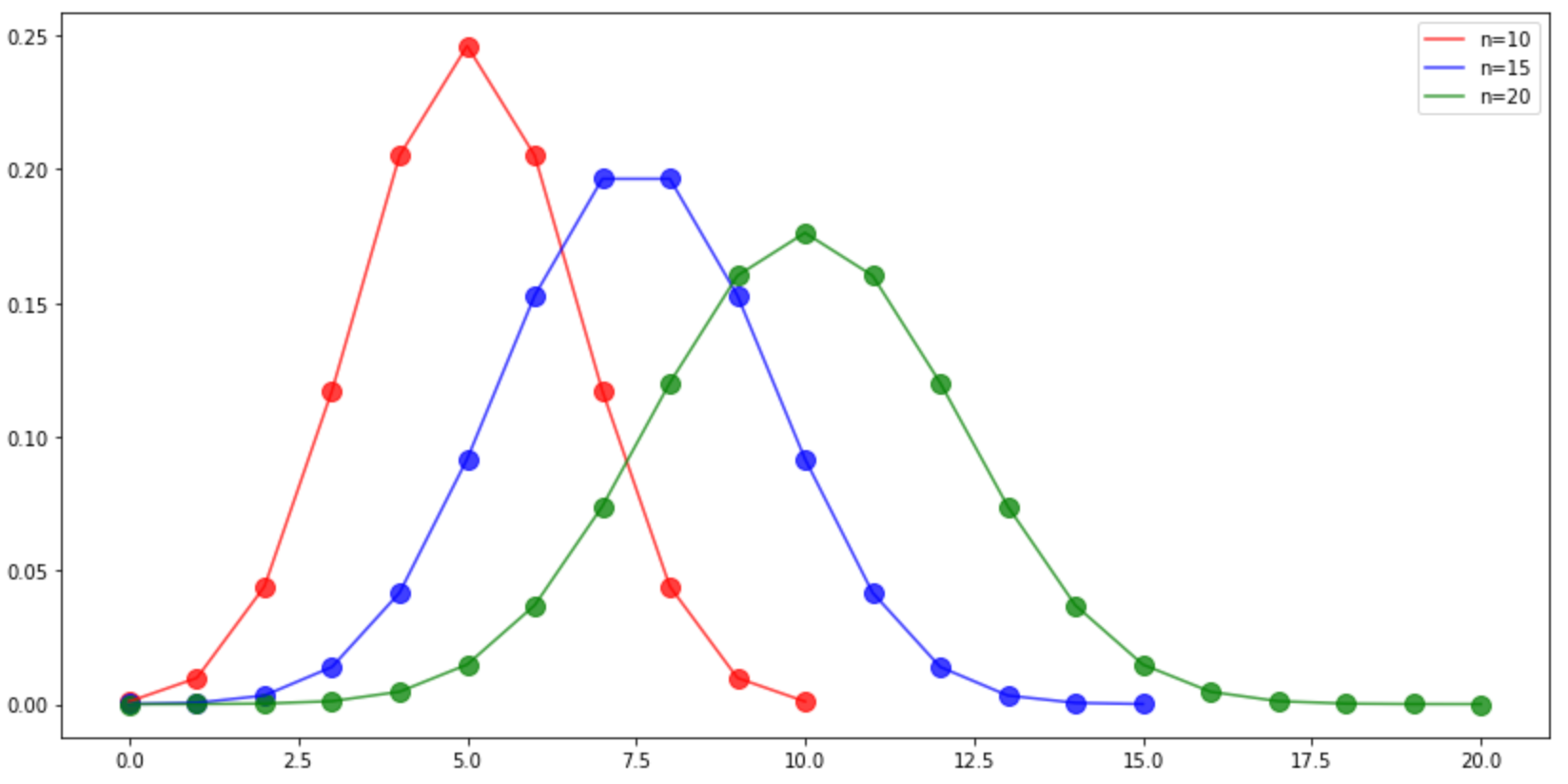
 试验总数的影响

plt.figure(figsize=(14,7))

#n=10
plt.scatter(np.arange(11),
            stats.binom.pmf(np.arange(11),p=0.5,n=10),
            alpha=0.75,
            color='r',
            s=100,
           )
plt.plot(np.arange(11),
         stats.binom.pmf(np.arange(11),p=0.5,n=10),
         alpha=0.75,
         color='r',
         label='n=10',
        )

#n=15
plt.scatter(np.arange(16),
            stats.binom.pmf(np.arange(16),p=0.5,n=15),
            alpha=0.75,
            color='b',
            s=100,
           )
plt.plot(np.arange(16),
         stats.binom.pmf(np.arange(16),p=0.5,n=15),
         alpha=0.75,
         color='b',
         label='n=15',
        )

#n=20
plt.scatter(np.arange(21),
            stats.binom.pmf(np.arange(21),p=0.5,n=20),
            alpha=0.75,
            color='g',
            s=100,
           )
plt.plot(np.arange(21),
         stats.binom.pmf(np.arange(21),p=0.5,n=20),
         alpha=0.75,
         color='g',
         label='n=20',
        )

plt.legend()
plt.show()

 随机样本

np.random.seed(0)

#进行10次试验，返回成功的次数
print(stats.binom.rvs(p=0.3,n=10),end='

')
#上面的试验进行11次
print(stats.binom.rvs(p=0.3,n=10,size=11),end='

')

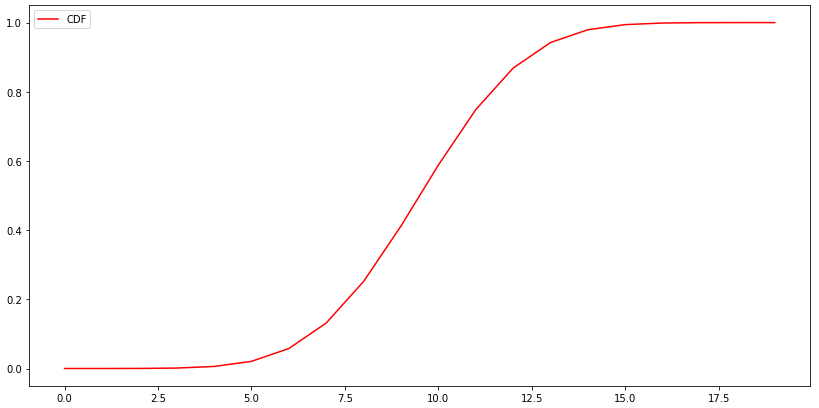
CDF

#CDF
plt.figure(figsize=(14,7))

plt.plot(np.arange(20),
         stats.binom.cdf(np.arange(20),p=0.5,n=20),
         color='r',
         label='CDF',
        )

plt.legend()
plt.show()

 区间计算

print('p(x<=3)={}'.format(stats.binom.cdf(k=3,p=0.3,n=10)))
print('p(2<x<=8)={}'.format(stats.binom.cdf(k=8,p=0.3,n=10)-stats.binom.cdf(k=2,p=0.3,n=10)))