题目:https://www.luogu.org/problemnew/show/P2900
题目描述
Farmer John is considering buying more land for the farm and has his eye on N (1 <= N <= 50,000) additional rectangular plots, each with integer dimensions (1 <= width_i <= 1,000,000; 1 <= length_i <= 1,000,000).
If FJ wants to buy a single piece of land, the cost is $1/square unit, but savings are available for large purchases. He can buy any number of plots of land for a price in dollars that is the width of the widest plot times the length of the longest plot. Of course, land plots cannot be rotated, i.e., if Farmer John buys a 3x5 plot and a 5x3 plot in a group, he will pay 5x5=25.
FJ wants to grow his farm as much as possible and desires all the plots of land. Being both clever and frugal, it dawns on him that he can purchase the land in successive groups, cleverly minimizing the total cost by grouping various plots that have advantageous width or length values.
Given the number of plots for sale and the dimensions of each, determine the minimum amount for which Farmer John can purchase all
约翰准备扩大他的农场,眼前他正在考虑购买N块长方形的土地。如果约翰单买一块土 地,价格就是土地的面积。但他可以选择并购一组土地,并购的价格为这些土地中最大的长 乘以最大的宽。比如约翰并购一块3 × 5和一块5 × 3的土地,他只需要支付5 × 5 = 25元, 比单买合算。 约翰希望买下所有的土地。他发现,将这些土地分成不同的小组来并购可以节省经费。 给定每份土地的尺寸,请你帮助他计算购买所有土地所需的最小费用。
输入输出格式
输入格式:
* Line 1: A single integer: N
* Lines 2..N+1: Line i+1 describes plot i with two space-separated integers: width_i and length_i
输出格式:
* Line 1: The minimum amount necessary to buy all the plots.
输入输出样例
说明
There are four plots for sale with dimensions as shown.
The first group contains a 100x1 plot and costs 100. The next group contains a 1x100 plot and costs 100. The last group contains both the 20x5 plot and the 15x15 plot and costs 300. The total cost is 500, which is minimal.
解析
在这个地方同时讲一下斜率优化,大佬们就请无视了吧。
注意:一定要看清横纵坐标是什么!!!!!!!!
很容易看出这是一道暴力题,然后我们超时了。
我们想一想该怎么做。
首先容易想到的一个优化便是:如果一片土地的长与宽都少于其他的一片土地,就把他排除。
所以我们先用长(设为x)排个序,假设从小到大吧,那么宽(设为y)会怎样呢?剔除不需要的后发现y单调递减。
比如:一开始拍完序后情况是这样的(横坐标x,纵坐标y),
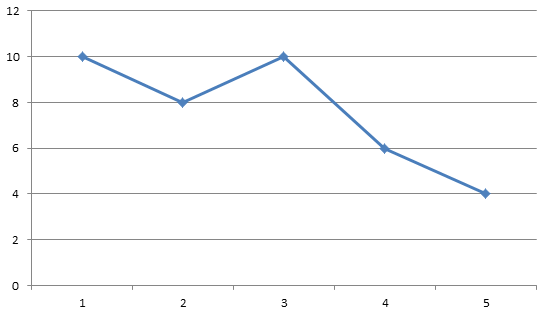
我们发现买了3*10的土地,就能把1*10的土地和2*8的土地包括了,所以前两个点就可以去掉,
情况就变成如下:(横坐标x,纵坐标y)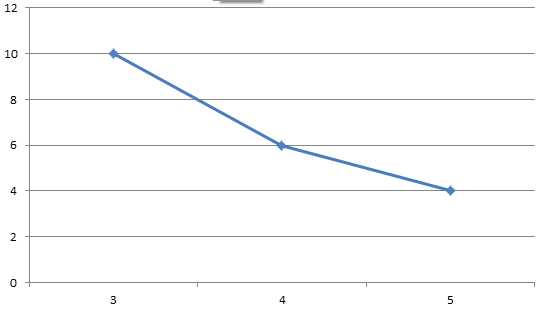
最后你会发现,保证合法的情况是单调递减的(这对后面考虑有点影响)。
剔除无用的数据之后,我们可以想到dp的思维。
我们来考虑最后选取的一个土地组合。
转移方程f[i]=f[j]+x[i]*y[j+1] 注意f[j]已经包括了x[j]*y[j],所以要乘y[j+1]。
然后开开心心地提交,期待actle的喜悦。
n*n复杂度跑50000,就是cf的评测集好像也过不了。
行了进入正题,我们要学习一种奇技淫巧叫做斜率优化。
转移方程f[i]=f[j]+x[i]*y[j+1],我们假设i由j和k转移过来(j<k<i),
那么k比较优的要求便是:
f[j]+x[i]*y[j+1] > f[k]+x[i]*y[k+1]
最后变形为(f[j]-f[k])/(y[j+1]-y[k+1])<-x[i],
发现左边同i无关,即可考虑乱搞一下了。
我们把这些点仍进一个双端队列里(具体为啥下面会讲)。
所以说这个式子又有什么卵用呢?
画几个图分析一下。
假设一个中间步骤,现在情况是这个样的。
注意:此时x轴为y(即宽度),y轴为f(即dp值),跟前面不一样
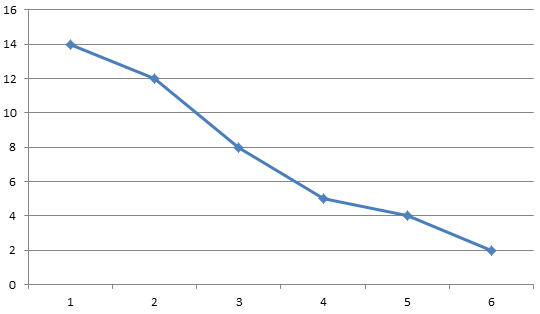
我们先从队首开始看。
队首的元素,取出q1和q2,此时q1,q2就相当于j,k两个转移点。
如果满足上述条件,也就是(f[q1]-f[q2])/(y[q1+1]-y[q2+1])<-x[i]时,由我们前面得到的结论,
可以知道用q1转移不如用q2转移了,然后就可以把队首元素残忍地抛弃,让下一个来当队首。
下一个当然也可能不如再下一个,所以用一个while处理队首的元素。
我们再考虑队尾的情况。
设s(a,b)=(f[q1]-f[q2])/(y[q1+1]-y[q2+1])。
所以队尾优化应该借鉴一下开头的写法。
然后你就没有什么思路了。
我们来研究一下s(j,k)和s(k,i)的情况(j<k<i)。
若s(j,k)<s(k,i):
①若s(j,k)<-x[i],那么k比j优,但由于s(j,k)<s(k,i)我们知道s(k,i)<-x[i],从而推出由k转移不如由i自己转移。
②若s(j,k)>=x[i],那么k就不必j优,k也是没用的了。
所以,当s(j,k)<s(k,i)时,我们就可以把k残忍地抛弃了。
具体表现就是满足条件就扔掉队尾,让队尾前一个当队尾,跟前面一样用个while。
两端排除没用的点使这种效率非常高。
我们再来看一下这个式子:(f[j]-f[k])/(y[j+1]-y[k+1])<-x[i],
因为x[i]我们排过序,是从左往右单调递增的,
我们再给他变个行(f[j]-f[k])/(y[k+1]-y[j+1])>x[i],
由于x[i]在递增,所以我们看出斜率的绝对值在越变越大。
最后大概图是这个样的,x轴代表y,y轴代表f[]。
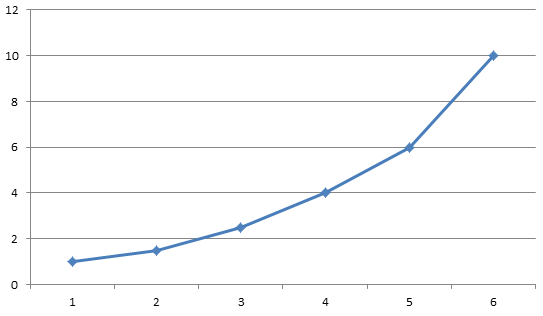
我们刚刚忙了那么多,就是为了维护这个单调递增的斜率绝对值。
专业术语好像叫做维护凸包。
我们就这样及时丢掉没用的点,节约了时间。复杂度O(n)。
好了说了这么多,上蒟蒻的代码吧。
不要忘了long long orz。

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 #include<queue> 7 using namespace std; 8 #define ll long long 9 const int maxn=50010; 10 struct node{ 11 ll x,y; 12 }a[maxn]; 13 bool cmp(const node &aa,const node &bb){ 14 return aa.x<bb.x; 15 } 16 ll n,cnt; 17 ll f[maxn]; 18 ll q[maxn],head,tail; 19 double k(ll aa,ll bb){ 20 return ((double)(f[aa]-f[bb]))/((double)(a[aa+1].y-a[bb+1].y)); 21 } 22 int main(){ 23 scanf("%lld",&n); 24 for (int i=1;i<=n;++i){ 25 scanf("%lld%lld",&a[i].x,&a[i].y); 26 } 27 sort(a+1,a+1+n,cmp); 28 for (int i=1;i<=n;++i){ 29 while (cnt&&a[i].y>=a[cnt].y) --cnt; 30 a[++cnt]=a[i]; 31 } 32 n=cnt; head=tail=1; 33 for (int i=1;i<=n;++i){ 34 while (head<tail&&k(q[head],q[head+1])>=-a[i].x) head++; 35 f[i]=f[q[head]]+a[i].x*a[q[head]+1].y; 36 while (head<tail&&k(q[tail-1],q[tail])<k(q[tail],i)) tail--; 37 q[++tail]=i; 38 } 39 printf("%lld",f[n]); 40 return 0; 41 }
