 粉樱花之恋
粉樱花之恋
链接:https://ac.nowcoder.com/acm/problem/18987
来源:牛客网
qn是个特别可爱的小哥哥,qy是个特别好的小姐姐,他们两个是一对好朋友 [ cp (划掉~)
又是一年嘤花烂漫时,小qn于是就邀请了qy去嘤花盛开的地方去玩。当qy和qn来到了田野里时,qy惊奇的发现,嘤花花瓣以肉眼可见的速度从树上长了出来。
仔细看看的话,花瓣实际上是以一定规律长出来的,而且,每次张成新的花瓣的时候,上一次的花瓣就会都落到地上,而且不会消失。
花瓣生长的规律是,当次数大于等于2时,第i次长出来的花瓣个数和上一次张出来的花瓣个数的差是斐波那契数列的第i-1项。初始的时候地上没有花瓣,树上的花瓣个数为1,第一次生长的花瓣个数为1。初始的那个花瓣就落到了地上
现在,小qn想知道,经过k次生长之后,树上和地上的总花瓣个数是多少?
ps:斐波那契数列:
f[1]=f[2]=1;f[i]=f[i-1]+f[i-2] (i>=2且i∈ N+)
输入描述:
一行一个数k
输出描述:
一行一个数m,表示第k次生长过后,树上和地上的总花瓣数是多少。由于答案会很大,请你将答案mod 998244353后输出
示例1
输入
4
输出
12
说明 第一次:树上1,地上1.第二次树上2,地上1+1,第三次树上3,地上1+1+2,第四次树上5,地上1+1+2+3。总共12个
示例2
输入
5
输出
20
说明 第五次树上8,地上1+1+2+3+5。总共20个
备注:
对于0%的数据,有k=样例
对于20%的数据,有k<=1’000
对于60%的数据,有k<=1’000’000
对于80%的数据,有k<=1’000’000’000
对于100%的数据,有k<1’000’000’000’000’000’000
(wa)思想:
直接看地上的花,是一个斐波那契数列之和,这时候可以使用矩阵的知识进行优化。(知识线性代数)
有些人对斐波那契数列为什么要用矩阵来做,这里给个例题:poj3073
我们都知道斐波那契数列后期速度以爆炸速度递增;所以运用了矩阵能够防止超时(递归次数过多)。
base = [ 1 1 ] 去乘 F = [ f(n+1)]
______ [ 1 0 ] ________[ fn ]
注意:此处的下划线仅用于调整版面位置。
相乘之后你会发现结果变成了
[ f(n+1)+fn ]
[ fn+1 ]
上面的就是我们需要的东西了;
错误思路:开始看乍一眼以为是斐波那契数列的累加,虽然用了矩阵进行优化结果只过了50%的数据。其实这种思路也没错,只不过数据有点苛刻
正确思想:(上面也要看噢,不然下面这可能看不懂
其实我们所需求的结果为 pow(base, n + 3)-1 (pow为第n位斐波那契数)
看来还是需要细心观察呀!!!!
记得在算法中间23行,要mod完全。
以下是常见的式子推导样例:
1.f(n)=a* f(n-1)+b*f(n-2)+c;(a,b,c是常数)
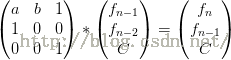
2.f(n)=c^n-f(n-1) ;(c是常数)
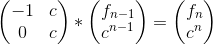
#include<iostream>
#include<cstdio>
using namespace std;
//const int maxn = 1e8 + 5;
#define ll long long
const ll mod = 998244353;
struct matrix
{
ll a[2][2];
};
//这里的mul和pow还有matrix要结合起来用,矩阵快速幂,题目中是有mod的
matrix mul(matrix &x, matrix &y) {//矩阵乘法
matrix c;
for (int i = 0; i<2; i++)
{
for (int j = 0; j<2; j++)
{
c.a[i][j] = 0;
for (int k = 0; k<2; k++)
c.a[i][j] = (c.a[i][j] % mod + ((x.a[i][k] % mod) * (y.a[k][j] % mod)) % mod)%mod;//这里需要mod
}
}
return c;
}
ll pow(matrix x, ll n) {//快速幂
matrix ans;
ans.a[0][0] = 1, ans.a[1][0] = 0;
ans.a[0][1] = 0, ans.a[1][1] = 1;
while (n)
{
if (n & 1)
ans = mul(ans, x);
x = mul(x, x);
n >>= 1;
}
return ans.a[0][1];
}
int main() {
ll n;
matrix base = { 1, 1, 1, 0 };
while (cin >> n && n != -1)
{
cout << pow(base, n + 3)-1 << endl;
}
return 0;
}