87 Eigen应用：解线性方程组的古典迭代法

0 引言

线性方程组的迭代法就是用某种极限过程逐步逼近线性方程组精确解的方法。迭代法具有需要的存储空间少、程序设计简单、原始系数矩阵在计算过程中始终不变等优点，但有收敛性或收敛速度的问题。迭代法是解大型稀疏矩阵方程组的重要方法。迭代法的基本思想是构造一串收敛到解的序列，即建立一种从已有近似解计算新的近似解的规则。由不同的计算规则得到不同的迭代法。

本文的主要思想来自于中南大学 郑洲顺 教授在中国大学MOOC上的 科学计算与数学建模 课程， 第六章 回归问题-线性方程组的迭代解法，链接如下。

https://www.icourse163.org/learn/CSU-1001985002?tid=1206784225#/learn/content?type=detail&id=1211843352&sm=1

1 问题的引入与定义

        

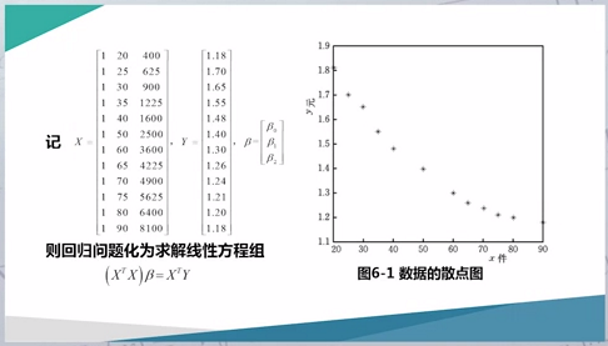
  求回归系数的本质是解线性方程组。迭代法解线性方程组的基本思路如下。

      

为了应用迭代法解线性方程组，首先应该找到一个迭代矩阵B，当k->无穷大时，误差->0，此时称该线性方程组迭代法收敛。值得一提的是，线性方程组迭代法的敛散性与具体的迭代矩阵有关。迭代矩阵不同，线性方程组迭代法的敛散性也有可能不同。 

2 线性方程组迭代法的收敛性

 

 直接给出结论如上。即当迭代矩阵的谱半径 < 1时，线性方程组时收敛的。由于谱半径时矩阵范数的下限，故存在如下迭代法收敛的充分条件。   

3 评价迭代法的优良

迭代矩阵谱半径可以衡量迭代矩阵的收敛速度，谱半径越小，迭代速度越快。

另外一个维度是精度。在保证精度的条件下，迭代的速度越快，认为算法的效果越好。

4 解线性方程组的古典迭代法-eigen实现

#include <iostream>
#include <Eigen/Dense>  // eigen library
#include <ctime>        // clock, etc
#include <iomanip>      // std::setprecision, etc
#include <cmath>        // use fabs, pow, etc
#include <climits>


/* 迭代法解线性方程组
* Ax = b
* 该迭代法收敛的必要条件有两条
*** 条件1：对角线元素不等于零
*** 条件2：0 < w < 2
* 迭代法解线性方程组的充要条件有一个
*** 谱半径 < 1 
* 
*/
enum IterativeSolverMethod{
    JACOBI,               // 雅可比迭代法
    GAUSS_SEIDEL,         // 高斯迭代法
    SOR                   // 超松弛迭代法
};
/* JacobiIterative: 雅可比迭代法解线性方程组
*/
void JacobiIterative(const Eigen::MatrixXd& A,     // 系数矩阵
                     const Eigen::VectorXd& b,      // 常数项 
                     Eigen::VectorXd& x){            // 解
    // 行遍历，每次迭代计算一个解
    Eigen::VectorXd x_temp = Eigen::VectorXd(x.size());
    for(int i = 0; i < A.rows(); ++ i){
        x_temp[i] = (b[i] - (A.row(i).dot(x) - x[i]*A(i, i)))/A(i, i);
    }
    x = x_temp;   // 全部算完再更新
}

/* GaussSeidelIterative: 高斯-赛达尔迭代法，雅克比迭代法的改进版本
* 区别在于，每次迭代计算一个新的解，均采用当前最新的结果
*/
void GaussSeidelIterative(const Eigen::MatrixXd& A,   // 系数矩阵
                          const Eigen::VectorXd& b,        // 常数项 
                          Eigen::VectorXd& x){             // 解
    // 行遍历，每次迭代计算一个解
    for(int i = 0; i < A.rows(); ++ i){
        x[i] = (b[i] - (A.row(i).dot(x) - x[i]*A(i, i)))/A(i, i);   // 实时更新
    }
}

/* SorIterative: 给定超松弛系数的超松弛迭代法
* 当w == 1时，就是Gauss-Seidel迭代法
*/
void SorIterative(const Eigen::MatrixXd& A,      // 系数矩阵
                  const Eigen::VectorXd& b,      // 常数项 
                  const double& w,               // 松弛因子w, 通常满足  0 < w < 2
                  Eigen::VectorXd& x){           // 解
    // 行遍历，每次迭代计算一个解
    for(int i = 0; i < A.rows(); ++ i){
        double x_gauss_seidel = (b[i] - (A.row(i).dot(x) - x[i]*A(i, i)))/A(i, i);  // Gauss-Seidel 迭代的结果
        x[i] = x[i] + w * (x_gauss_seidel - x[i]);
    }    
}
 
/* IterativeSolver: 选择迭代方法，根据阈值迭代求解线性方程组的解
*/
void IterativeSolver(const Eigen::MatrixXd& A,   // 系数矩阵
                     const Eigen::VectorXd& b,      // 常数项 
                     const int& threshold_iteration_times,            // 迭代次数
                     const double& threshold__iteration_error,        // 迭代误差
                     const IterativeSolverMethod& solver,                   // 迭代方法
                     Eigen::VectorXd& x){            // 解
    // x = Eigen::VectorXd::Zero(A.rows(), 1);  // 初始解
    x = Eigen::VectorXd::Zero(A.rows());  // 初始解
    Eigen::VectorXd last_x = x;   // 保存上一次的解用于计算两次迭代之间的误差

    // 判断是否满足迭代条件
    int current_iteration_times = 1;
    double current_iteration_error = static_cast<double>(INT_MAX);      // 借用INT_MAX对初始误差进行初始化

    const double w = 1.3;   // 在switch case外定义
    while(current_iteration_times < threshold_iteration_times &&  current_iteration_error > threshold__iteration_error){
        switch(solver){
            case JACOBI:
                JacobiIterative(A, b, x);
                break;
            case GAUSS_SEIDEL:
                GaussSeidelIterative(A, b, x);
                break;
            case SOR:
                SorIterative(A, b, w, x);
                break;
            default:
                break;
        }
        
        current_iteration_error = (x-last_x).norm();
        last_x = x;
        current_iteration_times ++;
    }
    std::cout << "current_iteration_error = (solution-last_solution).norm() = " << current_iteration_error << std::endl;
    std::cout << "current_iteration_times = " << current_iteration_times << std::endl;
}

void TestIterativeSolver(){
    const int dim = 4;
    Eigen::MatrixXd A(dim, dim);
    Eigen::VectorXd b(dim, 1);
    A << -4, 1, 1, 1,
        1, -4, 1, 1,
        1, 1, -4, 1,
        1, 1, 1, -4;
    b << 1, 1, 1, 1;

    // ldl分解求解精确值
    Eigen::VectorXd x_qr(dim, 1);
    x_qr = A.colPivHouseholderQr().solve(b);

    // 迭代法求解
    const int threshold_iteration_times = 100;        // 迭代次数
    const double threshold__iteration_error = std::pow(0.1, 4);    // 迭代误差

    Eigen::VectorXd x_jacobi_iteration;
    IterativeSolverMethod solver = JACOBI;
    IterativeSolver(A, b, threshold_iteration_times, threshold__iteration_error, solver, x_jacobi_iteration);

    Eigen::VectorXd x_gauss_seidel_iteration;
    solver = GAUSS_SEIDEL;
    IterativeSolver(A, b, threshold_iteration_times, threshold__iteration_error, solver, x_gauss_seidel_iteration);

    Eigen::VectorXd x_sor_iteration;
    solver = SOR;
    IterativeSolver(A, b, threshold_iteration_times, threshold__iteration_error, solver, x_sor_iteration); 

    std::cout << "x_qr = " << x_qr << std::endl;
    std::cout << "x_jacobi_iteration = " << x_jacobi_iteration << std::endl;
    std::cout << "absolute error of jacobi iteration is: " << (x_jacobi_iteration - x_qr).norm() << std::endl; 

    std::cout << "x_gauss_seidel_iteration = " << x_gauss_seidel_iteration << std::endl;
    std::cout << "absolute error of gauss seidel iteration is: " << (x_gauss_seidel_iteration - x_qr).norm() << std::endl; 

    std::cout << "x_sor_iteration = " << x_sor_iteration << std::endl;
    std::cout << "absolute error of SOR iteration is: " << (x_sor_iteration - x_qr).norm() << std::endl;    
}

int main()
{
    TestIterativeSolver();
    system("pause");
    return 0;
}

5 运行结果及分析

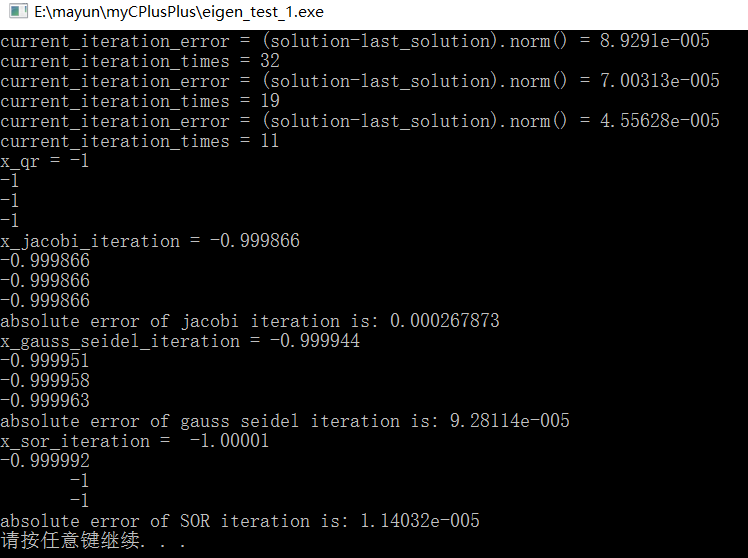
 如上图所示，采用Jacobi迭代法，Gauss-Seidel迭代法和超松弛迭代法解线性方程组的结果评价如下。

（1）从速度上来说，Jacobi迭代法 < Gauss-Seidel迭代法 < 超松弛迭代法

（2）从精度上来说，Jacobi迭代法 < Gauss-Seidel迭代法 < 超松弛迭代法

 因此，可以认为当w（松弛因子）选择合适的情况下，超松弛迭代法是最好的古典迭代法。