The Bad Luck Island is inhabited by three kinds of species: r rocks, s scissors and p papers. At some moments of time two random individuals meet (all pairs of individuals can meet equiprobably), and if they belong to different species, then one individual kills the other one: a rock kills scissors, scissors kill paper, and paper kills a rock. Your task is to determine for each species what is the probability that this species will be the only one to inhabit this island after a long enough period of time.
The single line contains three integers r, s and p (1 ≤ r, s, p ≤ 100) — the original number of individuals in the species of rock, scissors and paper, respectively.
Print three space-separated real numbers: the probabilities, at which the rocks, the scissors and the paper will be the only surviving species, respectively. The answer will be considered correct if the relative or absolute error of each number doesn't exceed 10 - 9.
2 2 2
0.333333333333 0.333333333333 0.333333333333
2 1 2
0.150000000000 0.300000000000 0.550000000000
1 1 3
0.057142857143 0.657142857143 0.285714285714


1 #include<stdio.h> 2 #include<queue> 3 #include<algorithm> 4 #include<string.h> 5 const double eps = 1e-13 ; 6 int r , s , p ; 7 const int M = 100 + 5 ; 8 double dp[M][M][M] ; 9 10 void work () 11 { 12 dp[r][s][p] = 1 ; 13 for (int i = r ; i >= 0 ; i --) { 14 for (int j = s ; j >= 0 ; j --) { 15 for (int t = p ; t >= 0 ; t --) { 16 if (i*j + j*t + t*i == 0) continue; 17 if (i) dp[i - 1][j][t] += dp[i][j][t] * i * t / (1.0 * (i * j + i * t + j * t)) ; 18 if (j) dp[i][j - 1][t] += dp[i][j][t] * j * i / (1.0 * (i * j +i * t +j * t)) ; 19 if (t) dp[i][j][t - 1] += dp[i][j][t] * t * j / (1.0 * (i * j + i * t + j * t )) ; 20 } 21 } 22 } 23 } 24 int main() 25 { 26 // freopen ("a.txt" , "r" , stdin ) ; 27 while (~ scanf ("%d%d%d" , &r , &s , &p)) { 28 memset (dp , 0 , sizeof(dp)) ; 29 work () ; 30 double sum = 0 ; 31 for (int i = 1 ; i <= r ;i ++) { 32 if (dp[i][0][0] > eps) { 33 sum += dp[i][0][0] ; 34 } 35 } 36 printf ("%.12f " , sum ); 37 int i ; 38 for (sum = 0 ,i = 1 ; i <= s ;i ++) { 39 if (dp[0][i][0] > eps) { 40 sum += dp[0][i][0] ; 41 } 42 } 43 printf ("%.12f " , sum ) ; 44 for (sum = 0 , i = 1 ; i <= p ;i ++) { 45 if (dp[0][0][i] > eps) { 46 sum += dp[0][0][i] ; 47 } 48 } 49 printf ("%.12f " , sum ) ; 50 } 51 return 0 ; 52 }
Let's count the values dp[r][s][p] — the probability of the situation when r rocks, s scissors and p papers are alive. The initial probability is 1, and in order to calculate the others we should perform the transitions.
Imagine we have r rocks, s scissors and p papers. Let's find the probability of the rock killing scissors (the other probabilities are calculated in the same way). The total number of the possible pairs where one species kills the other one is rs + rp + sp, and the number of possible pairs (rock, scissors) is rs. As all meetings are equiprobable, the probability we want to find is 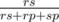 . This is the probability with which we go the the state dp[r][s — 1][p], with the number of scissors less by one.
. This is the probability with which we go the the state dp[r][s — 1][p], with the number of scissors less by one.
In the end, for example, to get the probability of the event that the rocks are alive, we should sum all values dp[i][0][0] for i from 1 to r (the same goes to the other species).