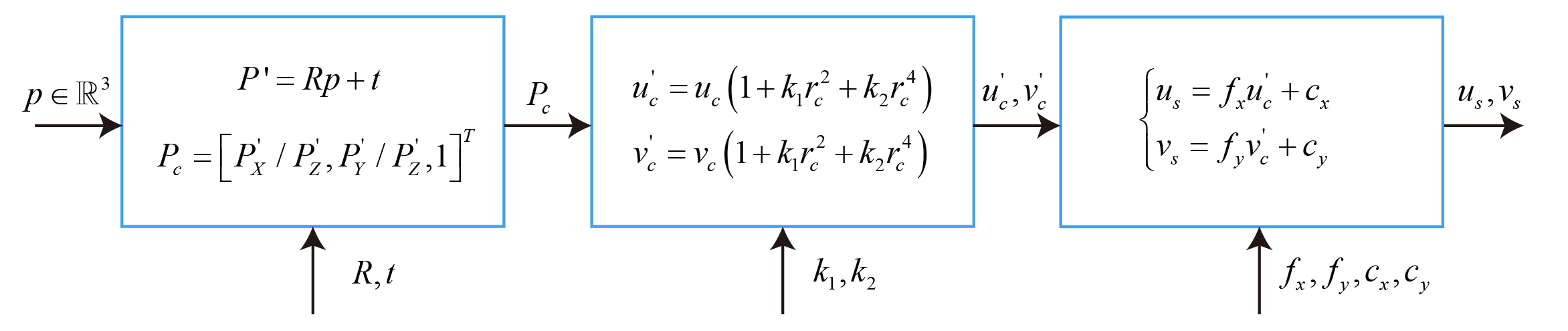BA(Bundle Adjustment),指从视觉图像中提取最优的路标3D模型和相机内外参数.
可以理解成,通过调整相机位姿和各个特征点的空间位置,使得路标特征点发出的光线聚焦到各处的相机光心,且光线穿过图像的各个特征点。
一、投影模型和BA代价函数
1. 回顾相机的成像过程
坐标转化过程:
- 世界坐标 → 相机坐标
\[\mathbf{P}' = \mathbf{R} \mathbf{p} + \mathbf{t} = [X', Y', Z']^T \]
相机坐标 → 归一化坐标
\[\mathbf{P}_c = [u_c, v_c, 1]^T = [X'/Z', Y'/Z', 1]^T \]归一化坐标 →去畸变归一化坐标
\[\left\{ \begin{array}{l} u_c' = {u_c}\left( {1 + {k_1}r_c^2 + {k_2}r_c^4} \right)\\ v_c' = {v_c}\left( {1 + {k_1}r_c^2 + {k_2}r_c^4} \right) \end{array} \right. \]
- 去畸变归一化坐标 →像素坐标
\[ \left\{ \begin{array}{l} {u_s} = {f_x}u_c' + {c_x}\\ {v_s} = {f_y}v_c' + {c_y} \end{array} \right. \]
相机的路标\(x\)和可以根据相机外参为\(R,t\)计算,对应的李群\(\xi\)和李代数\(T\):
路标点\(y\)即三维点p,观测数据是该点对应的像素坐标 \(\mathbf{z} \xlongequal{def} [u_s, v_s]^T\) ,那么观测方程可以写为:
然后把各个位置的误差累加,设\(z_{i,j}\)为位姿\(T_i\)处观察路标\(p_j\)产生的数据,那么代价函数为:
2. BA的求解
求解的话采用 牛顿法 和 列文伯格-马夸尔特法,具体的区别在于H取得是\(\mathbf{J }^T\mathbf{J}\) 还是 \(\mathbf{J}^T\mathbf{J}+ \lambda \mathbf{I}\)。
他们的增量方程为:
以牛顿法为例:
那么求解的关键在于\(J\)的求解。针对后端优化问题,变量\(x\)实际上是相机各个位置的外参和路标点:
其中对位姿的李代数\(\xi\)和路标空间\(p\)点分开表示 ,即:
那么代价函数可以表达为:
其中雅可比矩阵\(E\)和\(F\)是目标函数对\(x_c\)和\(x_p\)的导数,而损失的整体雅可比矩阵可以表达为:
那么牛顿法的近似海塞矩阵\(H\)可以表示成:
这是一个规模及其巨大的矩阵,如果我们直接对其求逆从而求解增量方程,所消耗的资源是非常大的。然而H具有稀疏性,利用这个性质我们可以加速求解过程。
2.1 \(H\)矩阵的稀疏性和边缘化
-
稀疏性
H的稀疏性由雅克比矩阵的稀疏性引起。考虑某个位置\(T_i\)处观测某个路标\(y_j\)的观测误差雅克比矩阵,
由于只和位姿\(T_i\)和路标\(y_j\)有关,因此\(e_{11}\)对随机变量位姿\(T_{\neq i}\) 和路标点 \(p_{\neq j}\)的偏导数应该为\(0\),即:
\[{J}_{ij}({x}) = \frac{\partial _{ij}}{\partial x} =\left( {0}_{2 \times 6},... {0}_{2 \times 6}, \frac{\partial {e}_{ij}}{\partial {T}_i}, {0}_{2 \times 6},... {0}_{2 \times 3},... {0}_{2 \times 3}, \frac{\partial {e}_{ij}}{ \partial {p}_j}, {0}_{2 \times 3},... {0}_{2 \times 3} \right) \]以例子 2个相机位姿\((C_1, C_2)\)和6个路标点\((P_1, P_2, P_3, P_4, P_5, P_6)\) 为例:
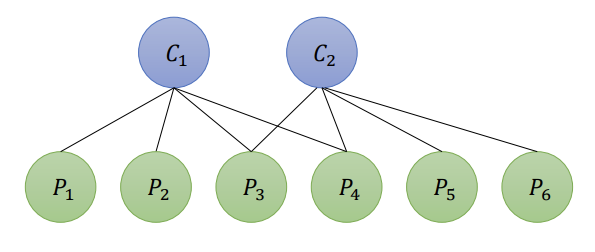 \[e = \frac{1}{2} \left( {e}_{11}^2 + {e}_{12}^2 + {e}_{13}^2 + {e}_{14}^2 + {e}_{23}^2 + {e}_{24}^2 + {e}_{25}^2 + {e}_{26}^2 \right) \]
\[e = \frac{1}{2} \left( {e}_{11}^2 + {e}_{12}^2 + {e}_{13}^2 + {e}_{14}^2 + {e}_{23}^2 + {e}_{24}^2 + {e}_{25}^2 + {e}_{26}^2 \right) \]以\(e_{11}\)为例,记\(J_{11}\)为\(e_{11}\)的雅可比矩阵,我们把所有变量以 \(x = (ξ_1,ξ_2,p_1,…,p_6)^T\) 的顺序摆放,则有:
\[{J}_{11} = \frac{\partial {e}_{11}}{\partial {x}} = \left( \frac{\partial {e}_{11}}{\partial {\xi}_1}, {0}_{2\times 6}, \frac{\partial {e}_{11}}{\partial {p}_1}, {0}_{2\times 3}, {0}_{2\times 3}, {0}_{2\times 3}, {0}_{2\times 3}, {0}_{2\times 3} \right) \]为了方便表示稀疏性,我们用带有颜色的方块表示矩阵在该方块内有数值,其余没有 颜色的区域表示矩阵在该处数值都为 0。用图像表征如下:
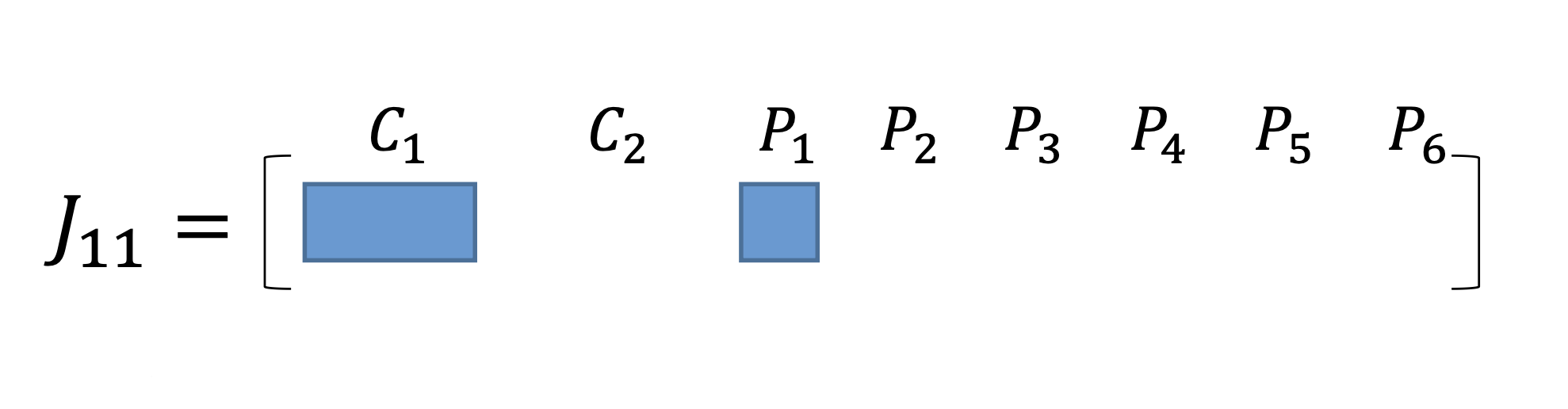
为了得到该目标函数对应的雅可比矩阵,那么整体雅可比矩阵以及相应的 H 矩阵的稀疏情况:
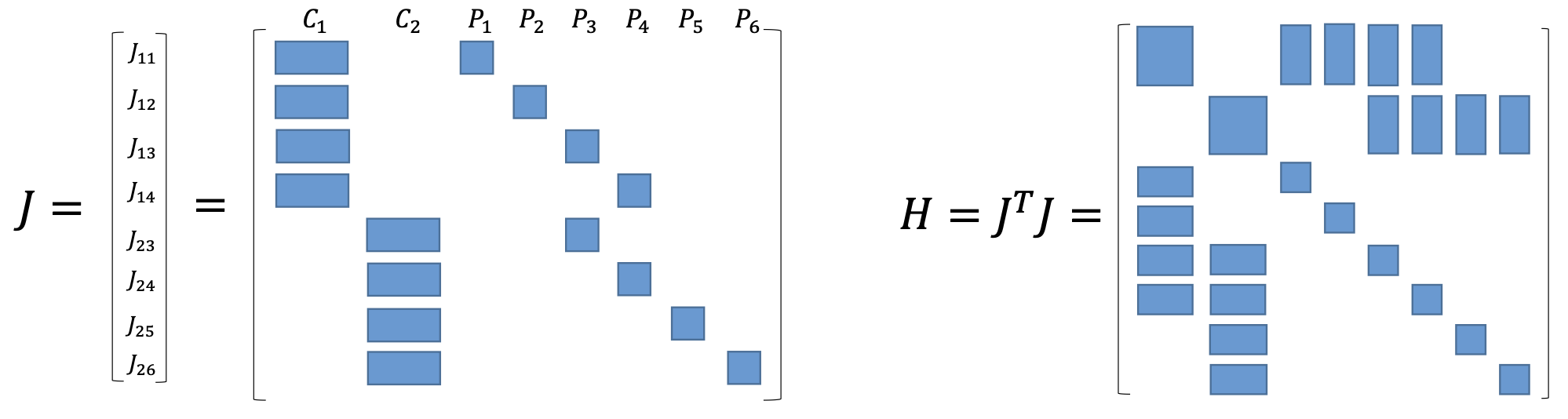
由于通常 路标数量 \(\ggg\) 相机位姿,它的左上角块显得非常小,而右下角的对角块占据了大量地方。由于它的形状很像箭头,又称为箭头形矩阵。
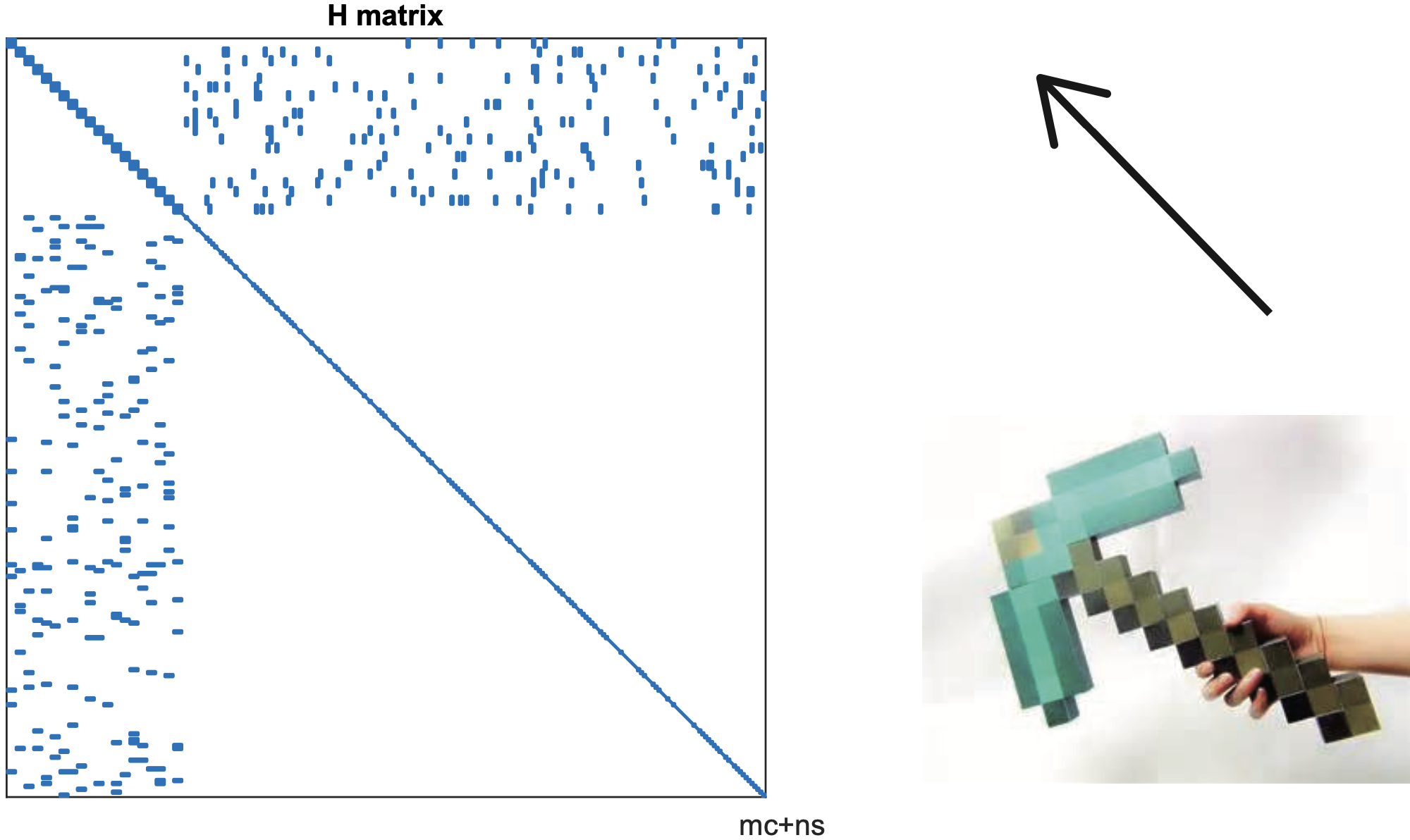
对于这样子的稀疏矩阵H,高斯法对稀疏矩阵直接求逆比较耗时,其加速在SLAM中称为边缘化,可以用Schur消元法求解。
-
边缘化(Marginalization)
即利用加速手段,求解\(Hx=-b\)
如下图,把H矩阵分为的四块分别记作如下 :
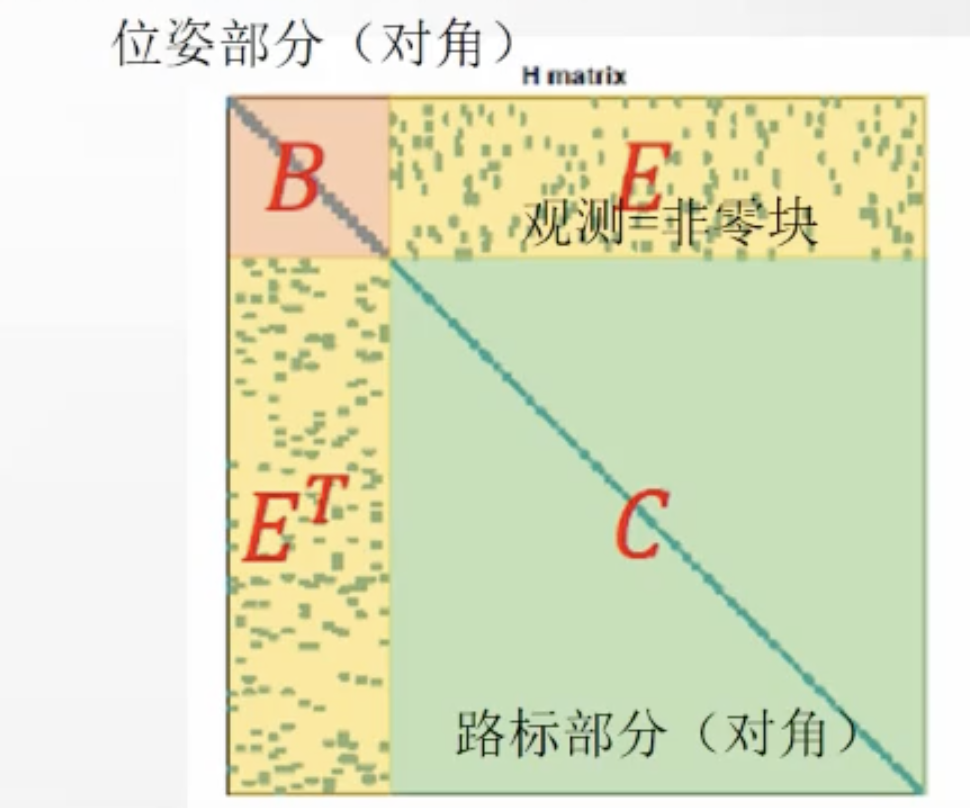
该矩阵\(J^TJ\)具有如下特点:
- 对于非对角线部分如果非零,可以理解为对应的两个变量检存在约束;
- 是对称矩阵
- B方阵对应的尺寸为相机位姿的数量m,相对较小
- C方针对应的尺寸为路标点的数量n,相对较大
- 相机运动速度越快,E中相机和路标点的关联性越小,矩阵越系数
可以描述成:
\[H=\begin{bmatrix} {B} & {E} \\ {E^T} & {C} \end{bmatrix} \]利用C对E进行高斯消元:
\[\left[ \begin{matrix} {I} & -{EC^{-1}} \\ {0} & {I} \end{matrix}\right] \left[ \begin{matrix} {B} & {E} \\ {E^T} & {C} \end{matrix}\right] \left[ \begin{array}{l} \Delta {x}_c \\ \Delta {x}_p \end{array} \right] = \left[ \begin{matrix} {I} & -{EC^{-1}} \\ {0} & {I} \end{matrix} \right] \left[ \begin{array}{l} {v} \\ {w} \end{array} \right] \]整理可以得到:
\[ \left[ \begin{matrix} {B} - {E}{C}^{-1}{E}^T & {0} \\ {E}^T & {C} \end{matrix} \right] \left[ \begin{array}{l} \Delta {x}_c \\ \Delta {x}_p \end{array} \right] = \left[\begin{array}{l} {v} - {E}{C}^{-1}{w} \\ {w} \end{array}\right]. \]用第一行计算出 \(\Delta {x}_c\)的值,再带入第二行,求解 \(\Delta {x}_p\)。由于x_c的维度通常较小(十位数量级)。
优点:相比直接求H的逆,转而求C的逆,大幅降低了解算难度。
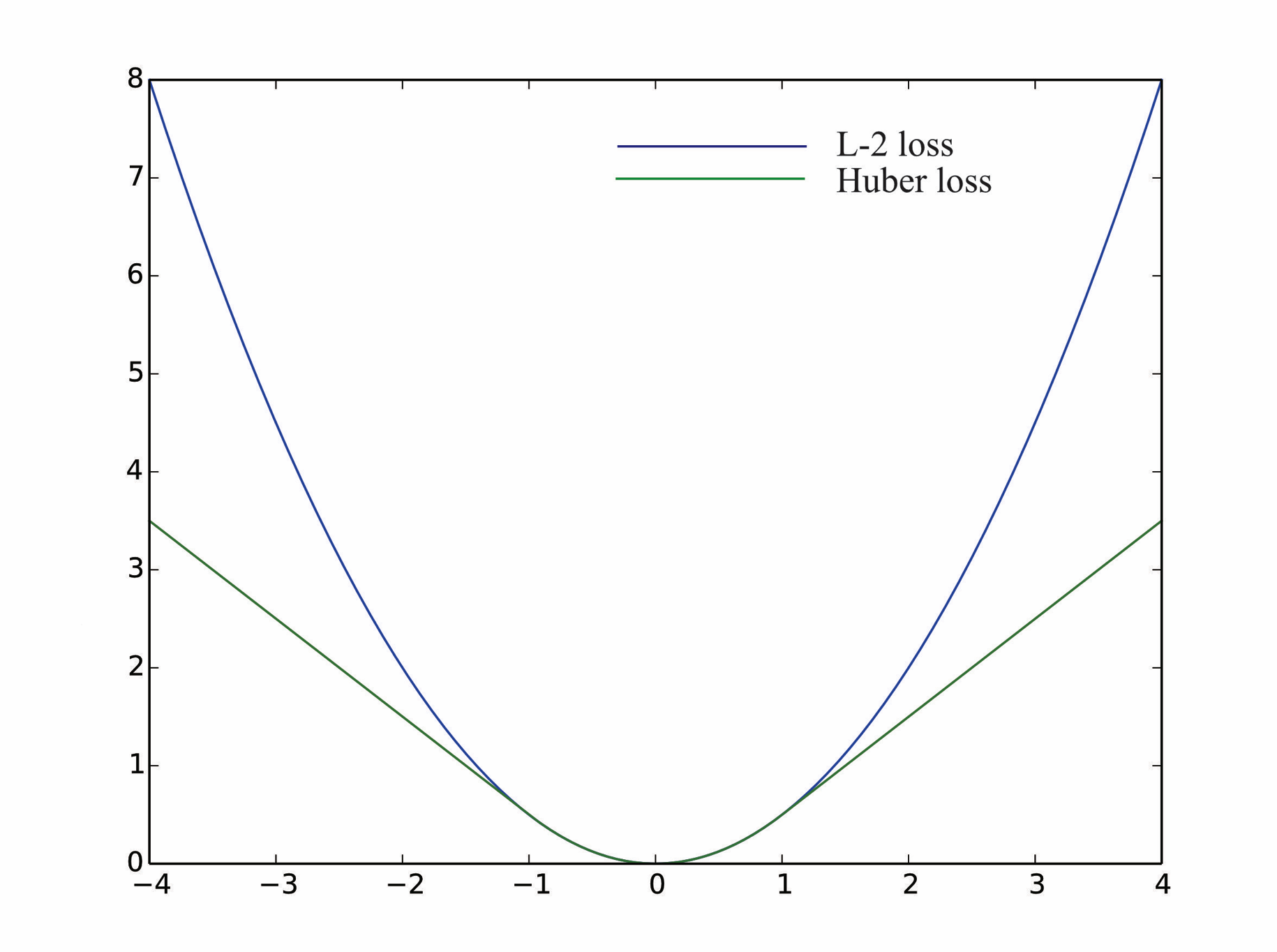
2.2 鲁棒核函数
当输入的数据存在较大服务误差时,在二范式中产生的梯度也会很大,从而导致增量朝着错误的方向变化。选用一个具有光滑性质并且变化较小的函数可以使得系统更稳健,这种函数称为鲁棒核函数。
Huber核函数(对误差从二次项变成一次项):