本系列为李航《统计学习方法》学习笔记整理,以下为目录:
(一)统计学习方法概论
(二)感知机
(三)k近邻
(四)朴素贝叶斯
(五)决策树
(六)逻辑斯蒂回归与最大熵模型
(七)支持向量机
(八)提升方法
(九)EM算法及其推广
(十)隐马尔科夫模型
(十一)条件随机场
第一章 统计学习方法概论
统计学习的对象是数据,关于数据的基本假设是同类数据具有一定的统计规律性。
· 特点:
数据独立同分布;模型属于某个假设空间(学习范围);给定评价准则下最优预测;最优模型的选择由算法实现
1.2 监督学习
给定有限训练数据出发,假设数据独立同分布,而且假设模型属于某个假设空间,应用某已评价准则,从假设空间中选择一个最优模型,使它对已给训练数据及未知测试数据在评价标准下有最准确的预测。
· 监督学习:分类、标注(序列预测)和回归
· 概念
输入空间、特征空间和输出空间
联合概率分布
假设空间
1.3 三要素
a. 模型
模型就是所要学习的条件概率分布(非概率模型)或决策函数(概率模型)
b. 策略
统计学习的目标在于从假设空间中选取最优模型。
损失函数来度量预测错误的程度,损失函数的期望是
学习目标是选择期望风险最小的模型。
· 学习策略(选择最优化的目标函数):
1) 经验风险最小化
极大似然估计
2) 结构风险最小化(在经验风险上添加模型复杂度的正则化项,防止过拟合)
贝叶斯中的最大后验概率估计MAP
c. 算法- 最优化求解问题
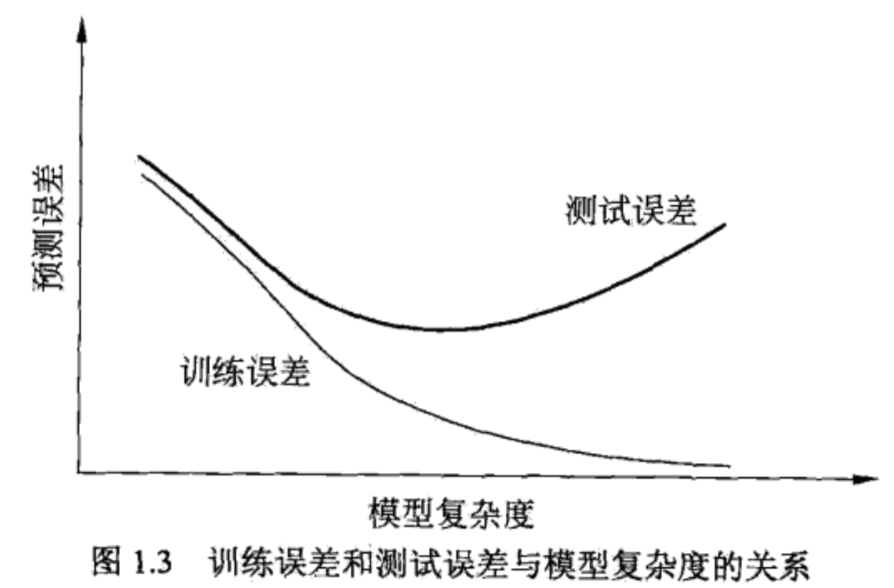
1.4 模型评估与选择
训练误差和测试误差
过拟合
1.5 正则化与交叉验证(模型选择方法)
正则化符合奥卡姆剃刀原理;从贝叶斯估计的角度来看,正则化项对应模型的先验概率,复杂的模型具有较大先验概率。
交叉验证:简单、S折和留一交叉验证;
1.6 泛化能力
如果学到的模型是f,那么对未知数据的预测误差为泛化误差(期望风险):
对于二分类问题,训练误差小的模型,泛化误差也会小?
1.7 生成模型与判别模型
生成方法(generative approach) 由数据学习联合概率分布P(X,Y),然后求出条件概率分布P(Y|X)作为预测的模型 P(Y|X) = P(X, Y)/ P(X)
模型给定了输入X产生输出Y的生成关系。典型的有朴素贝叶斯和隐马尔可夫
判别方法(discriminate approach)由数据直接学习决策函数或条件概率分布。典型的有k近邻,感知机,决策树,最大熵,SVM等