1.多项式
定义 (F(x)) 表示一个 (n-1) 次的多项式(其实你可以把多项式理解为方程)。
则 (F(x) = a_0x^0 + a_1x^1 + a_2x^2+...a_{n-1}x^{n-1}) ,即 (F(x) =displaystylesum_{i=0}^{n-1}a^ix^i)。
这也就是我们经常用的系数表示法(初中应该都学过吧)。
2.点值表示法
在介绍 (FFT) 之前,有必要接触一下这种方法。
首先我们可以知道 (n) 个点可以确定一个 (n-1) 次的多项式,因为你可以通过各种消元得到每一次的系数。
如 (F(x) = x^2+3x+1) . 我们就可以用点值表示法表示为 ((0,1),(1,5),(-1,-1)).
3.多项式乘法
其实多项式乘法就是卷积的形式。
假如我们有两个多项式 (A(x)) 和 (B(x)), 其中 (A(x) = a_0x^0+a_1x^1+a_2x^2....a_{n-1}x^{n-1}), (B(x) = b_0x^0+b_1x^1+b_2x^2....b_{m-1}x^{m-1})
显然如果 (A(x) imes B(x) = C(x)) ,那么 (C_i = displaystylesum_{i=0}^{i}a_ib_{i-j}).
这样直接乘的复杂度是 (O(n^2)) 的,下面要讲的 (FFT) 则可以使他变为 (O(nlogn))。
4.FFT
这个就是我们今天的主角,它的全称叫 快速离散傅里叶变化,据说傅里叶大神在计算机发明的100多年前就发明了这个算法。
下面我们来看看他是具体怎么操作的。
假如说我们已经知道了 (A(x)) 和 (B(x)) 在 (x_0) 处的取值,那么 (C(x)) 在 (x_0) 处的取值直接把两个数相乘就可以得到。
间接地我们就知道了 (C(x)) 的点值表示法。
来后整个 (FFT) 的流程我们就大致知道了:
- 求值,分别求出多项式 (A(x),B(x)) 的点值表示法
- 相乘,把 (A(x),B(x)) 的点值乘起来,得到 (C(x)) 的点值表示法 。
- 插值,把 (C(x)) 的点值表示法转化为系数表示法。
中间第二部相乘,显然可以做到 (O(n)) 的来写。第一步朴素算法就是找 (n) 个不同的值分别代入方程中,复杂度为 (O(n^2)) 的,第三部复杂度就更槽糕了,直接高斯消元的话复杂度直接变为 (O(n^3)) 的,这比直接相乘的暴力还要慢,显然还需要继续优化。
运用点值表示法,我们可以任意选 (n) 个数代进去,这启发我们从这里入手开始优化,那么傅里叶大神也注意到了这一点,把复数和单位根引进了这个方程中。
5.单位根及其性质
在了解把复数和单位根引入这个方程有什么用前,要先了解一下,单位根的性质。
首先,单位根所在的点就是把单位圆平均分为 (n) 份的分割点,也就是一个向量。
我们一般从 ((0,1)) 开始逆时针开始标号得到 (w_{n}^{0},w_{n}^{1}...w_{n}^{n-1}),,
例如八次单位根
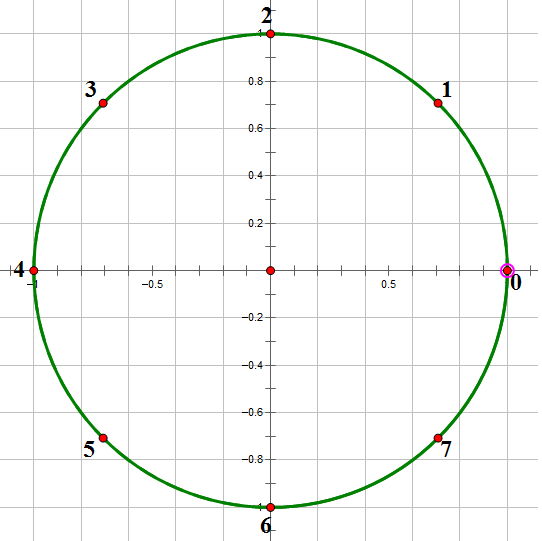
单位根有如下几条性质:
性质1: (w_{n}^{k} = (w_{n}^{1})^k)
证明:
(w_{n}^{k} imes w_{n}^{1} = (cos{kover n}2π,sin{nover k}2π) * (cos{1over n}2π,sin{1over n}2π))
(=(cos{kover n}2π imes cos{1over n}2π-sin{nover k}2π imes sin{1over n} 2π,cos{kover n}2π imes sin{1over n}2π-sin{kover n}2π imes cos{1over n}2π)
(=(cos({kover n}+{1over n})2π,sin({kover n}+{1over n})2π))
(=(cos{{k+1}over n}2π,sin{{k+1}over n}2π))
(= w_{n}^{k+1})
至于第二步怎么转化过来的,具体可以看一下 和角公式 。
性质2: ((w_{n}^{x})^{y} = w_{n}^{x*y})
证明:
首先我们有 ((a^x)^y = a^{x*y}) ,
然后就有 ((w_{n}^{x})^y = ((w_n^{1})^x)^y = (w_{n}^{1})^{x*y} = w_{n}^{x*y}).
性质3: (w_{n*x}^{k*x} = w_{n}^{k})
证明:
(w_{n*x}^{k*x} = (cos{k*xover{n*x}}2π,sin{k*xover{n*x}}2π))
(=cos_{n}^{k}2π,sin_{n}^{k}2π) (约分大法好)
(=w_{n}^{k})
性质4: 如果 (n) 为偶数,则 (w_{n}^{k} = -w_{n}^{k+{nover 2}})
证明:
你观察一下上面的那个图就会发现, (w_n^{k+{nover 2}}) 所表示的向量其实是 (w_n^{k}) 这个向量旋转 180 度之后得到的。
然后仔细观察一下他们好像关于原点对称,那么自然满足 (w_{n}^{k} = -w_{n}^{k+{nover 2}}).
数学证明:
(-w_{n}^{k+{nover 2}} = -(cos({k+{nover 2}over n})2π,sin({{k+{nover 2}}over {n}}2π))
(=-(-cos{kover n}2π,-sin{kover n}2π))
(=(cos({kover n}2π,sin{kover n}2π))
$=w_{n}^{k} $
诱导公式nb, (cos(x+π) = -cos x), (sin(x+π) = -sin(x+π))。
6.插值优化
既然单位根有那么多的性质,那么把他代入方程会产生神马化学反应呢?
第一点就是比较方便插值。
首先 (F(x)) 的离散傅里叶变换指把 (w_n^{0},w_{n}^{1}....w_{n}^{n-1}) 作为多项式(方程)的 (x) 代入得到 ((y_0,y_1...y_{n-1})) ,实际上他是一个插值的过程。
然后现在有一个结论:
对一个多项式进行离散傅里叶变换得到的 ((y_0,y_1...y_{n-1})) 作为系数组成一个新的多项式 (B(x)),然后把 (n) 个单位根 (w_n^{0},w_{n}^{1}....w_{n}^{n-1}) 取倒数代入得到 ((z_0,z_1....z_{n-1})) , 那么 (A(x)) 第 (i) 项的系数就是 (z_{i}) 除以 (n) 的结果。
具体来说就是:
(A(x) = a_0x^0+a_1x^1+a_2x^2...a_{n-1}x^{n-1})
将 (w_n^{0},w_{n}^{1}....w_{n}^{n-1}) 分别作为 (x) 代入求值得到 ((y_0,y_1...y_{n-1}))
(B(x) = y_0x^0 + y_1x^1+y_2x^2+y_{n-1}x^{n-1})
然后再把 ((w_{n}^{-1},w_{n}^{-2}...w_{n}^{-(n-1)})) 作为 (x) 代入求值,得到 ((z_0,z_1.....z_{n-1}))
最后 (z_k = a_{k}*n)
证明:
(z_k = displaystylesum_{i=0}^{n-1}y_i * (w_{n}^{-k})^i)
(=displaystylesum_{i=0}^{n-1}(w_{n}^{-k})^i(sum_{j=0}^{n-1}a_j * (w_{n}^{i})^j ))
(=displaystylesum_{i=0}^{n-1}sum_{j=0}^{n-1}a_j*(w_{n}^{i})^j * (w_{n}^{-k})^i)
(=displaystylesum_{i=0}^{n-1}sum_{j=0}^{n-1}a_j*w_n^{i*j} * w_n^{-k*i})
(=displaystylesum_{i=0}^{n-1}sum_{j=0}^{n-1}a_j*w_{n}^{i*(j-k)})
(=displaystylesum_{j=0}^{n-1}a_j sum_{i=0}^{n-1}(w_n^{j-k})^i)
对于 (displaystylesum_{i=0}^{n-1}(w_n^{j-k})^i) 我们发现,当 (j ==k) 的时候,这个值等于 (n) .
其他情况下这个值都为 (0) ,这个需要用等比序列求和来做。
首先,把求和项展开可以发现是一个公比为 (w_n^{j-k}) 的一个等比序列,利用求和公式可得:
(displaystylesum_{i=0}^{n-1}(w_n^{j-k})^i = {(w_{n}^{j-k})^n -1over w_{n}^{j-k}-1} = {(w_{n}^{n})^{j-k}-1over w_n^{j-k}-1} = {1^{j-k}-1over w_n^{j-k}-1} = 0)
因此 (z_k = a_k * n).
所以,我们利用离散傅里叶变换,把插值就变为了一次求值的过程,现在主要是解决求值的问题。
7.求值优化
首先我们定义一个多项式 (A(x) = a_0x^0+a^1x^1+a^2x^2....a_{n-1}x^{n-1}), 然后要求的是把 (w_{n}^{0},w_{n}^{1}....w_{n}^{n-1}) 代入后的结果。
这个到底怎么做的,我们现在引进快速傅里叶变换。
它主要把次数按奇偶项分类进行处理。
比如: (A(x) = (a_0x^0+a_2x^{2}+a_4x^4.....) + (a_1x^1+a_3x^3+a^5x^5......))
设 (A1(x) = a_0x^0+a^2x^1+a_4x^2.....) , (A2(x) = a_1x^0+a_3x^1+a_5x^2...)
显然 (A(x) = A1(x^2) + xA2(x^2))
然后我们尝试把单位根代入
如果 (这个值 < {nover 2}) ,我们直接把 (k) 代入得:
(A(w_n^{k}) = A1(w_n^{2k}) + w_n^{k}A2(w_n^{2k}) = A1(w_{nover 2}^{k}) + w_{n}^{k}A2(w_{nover 2}^{k})))
如果 $这个值geq {nover 2} $,我们把 (w_{n}^{k+{nover 2}}) 代入可得:
(A(w_{n}^{k+{nover 2}}) = A1(w_{n}^{2k+n})+w_{n}^{k+{nover 2}}A2(w_{n}^{2k+n}) = A1(w_{n}^{2k}*w_{n}^{n}) - w_{n}^{k}A2(w_{n}^{2k}*w_{n}^{n}) = A1(w_{nover 2}^{k})-w_{n}^{k}A2(w_{nover 2}^k))
假如你知道 (A1(x)) 和 (A2(x)) 代入 (w_{nover 2}^{0},w_{nover 2}^{1}....w_{nover 2}^{{nover 2}-1}) 的结果,那么 (A(x)) 代入 (w_{n}^{0},w_{n}^1....w_{n}^{n-1}) 的值我们就可以 (O(n)) 的得出来了。
我们可以一直递归下去,直到 (n=0) 时,柿子的值就是 (w_n^0 imes 系数) ,就可以直接 (return) 了。
复杂度 (T(n) = 2*T({nover 2})+O(n) = nlog n)
下面给出 FFT 递归的实现版本
void FFT(complex *a,int len,int flag)
{
if(len == 1) return;//只有一次项的时候停止递归
int A1[N],A2[N];
for(int i = 0; i < len; i += 2)//按奇偶的奇偶分类递归
{
A1[i>>1] = a[i];
A2[i>>1] = a[i+1];
}
FFT(A1,len>>1,flag); FFT(A2,len>>1,flag);//递归计算 A1(x),A2(x)
complex wn = {cos(Pi/len),flag * sin(Pi/len)};//单位根
for(int i = 0; i < len>>1; i++)
{
complex u = A1[i];
complex v = w * A2[i];
a[i] = u + v;
a[i+(len>>1)] = u-v;
w = w * wn;//下一个单位根
}
}
8.递归转迭代
上面那么伪代码是不可以通过模板的,主要是递归的时候计算耗费了大量的常数。
一个比较好的优化方法就是递归转迭代。
有位大神发现 FFT 递归的时候有个性质,就是对于 (a_x) 他最后的位置就是把 (x) 的二进制位翻转的位置。
比如 (4(100)->2(001)) ,可以结合图理解一下:

这样我们可以 (O(n)) 的预处理处每个 (ax) 最后的系数,然后就可以借助非递归快速实现了。
总代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 5e6+10;
const double Pi = acos(-1.0);
int n,m,len,tim,Rev[N];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
struct complex//定义一个复数
{
double x,y;
// complex(double a,double b){x = a, y = b;}
}a[N],b[N];
complex operator + (complex a, complex b){return (complex){a.x+b.x,a.y+b.y};}//重载复数的各种操作
complex operator - (complex a, complex b){return (complex){a.x-b.x,a.y-b.y};}
complex operator * (complex a, complex b){return (complex){a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
void FFT(complex *a,int flag)
{
for(int i = 0; i < len; i++)
{
if(i < Rev[i]) swap(a[i],a[Rev[i]]);
}
for(int h = 1; h < len; h <<= 1)//从下往上开始合并,枚举这次合并的区间长度的一半是多少
{
complex wn = complex{cos(Pi/h),flag*sin(Pi/h)};//单位根
for(int j = 0; j < len; j += (h<<1))//枚举这一层每一组的起始位置
{
complex w = complex{1,0};
for(int k = 0; k < h; k++)//处理每一组的值
{
complex x = a[j+k];
complex t = w * a[j+k+h];
a[j+k] = x+t;
a[j+k+h] = x-t;
w = w * wn;
}
}
}
}
int main()
{
n = read(); m = read();
for(int i = 0; i <= n; i++) a[i].x = read();
for(int i = 0; i <= m; i++) b[i].x = read();
len = 1, tim = 0;
while(len <= n+m) len <<= 1, tim++;
for(int i = 0; i < len; i++) Rev[i] = (Rev[i>>1]>>1) | ((i&1)<<(tim-1));//预处理每个系数最后的位置,只可意会不可言传
FFT(a,1); FFT(b,1);
for(int i = 0; i < len; i++) a[i] = a[i] * b[i];
FFT(a,-1);
for(int i = 0; i <= n+m; i++) printf("%d ",(int) (a[i].x/len+0.5));
printf("
");
return 0;
}