P2607 [ZJOI2008]骑士
题目描述
Z 国的骑士团是一个很有势力的组织,帮会中汇聚了来自各地的精英。他们劫富济贫,惩恶扬善,受到社会各界的赞扬。
最近发生了一件可怕的事情,邪恶的 Y 国发动了一场针对 Z 国的侵略战争。战火绵延五百里,在和平环境中安逸了数百年的 Z 国又怎能抵挡的住 Y 国的军队。于是人们把所有的希望都寄托在了骑士团的身上,就像期待有一个真龙天子的降生,带领正义打败邪恶。
骑士团是肯定具有打败邪恶势力的能力的,但是骑士们互相之间往往有一些矛盾。每个骑士都有且仅有一个自己最厌恶的骑士(当然不是他自己),他是绝对不会与自己最厌恶的人一同出征的。
战火绵延,人民生灵涂炭,组织起一个骑士军团加入战斗刻不容缓!国王交给了你一个艰巨的任务,从所有的骑士中选出一个骑士军团,使得军团内没有矛盾的两人(不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况),并且,使得这支骑士军团最具有战斗力。
为了描述战斗力,我们将骑士按照 (1) 至 (n) 编号,给每名骑士一个战斗力的估计,一个军团的战斗力为所有骑士的战斗力总和。
输入格式
第一行包含一个整数 (n),描述骑士团的人数。
接下来 (n) 行,每行两个整数,按顺序描述每一名骑士的战斗力和他最痛恨的骑士。
输出格式
应输出一行,包含一个整数,表示你所选出的骑士军团的战斗力。
输入输出样例
输入 #1
3
10 2
20 3
30 1
输出 #1
30
说明/提示
数据规模与约定
对于 30% 的测试数据,满足(n le 10);
对于 60% 的测试数据,满足 (n le 100);
对于 80% 的测试数据,满足(n le 10 ^4)。
对于 100% 的测试数据,满足 (1le n le 10^6),每名骑士的战斗力都是不大于 (10^6) 的正整数。
首先,我们对于互相憎恨的骑士连一条双向边,然后我们就可以求全图的最大独立子集(只相邻的点不能同时被选)。
就转化为了类似于上司的舞会那道题。
就有转移 (f[x][0] += max(f[to][0],f[to][1])), (f[x][1] += f[to][0])
(f[x][0/1]) 表示 在以 (x) 为根的子树中选或不选 (x) 节点得到的最大权值。
可这可能会出现环的情况,变成基环树或者基环树森林。
这,我们还是按照套路,找出每个环,然后断掉环上的一条边,在对整颗树做一遍树形(dp) 就可以得到答案。
一个比较好的优化就是 我们只需要枚举断掉的环上的两个端点,在对整棵树跑一边 (dp).
而不至于对每条边的端点都跑一遍。
因为当你这个点的状态确定的话,后面所有点的状态都会是确定的(可以感性理解一下)。
最后再说一下比较坑的一个点:
-
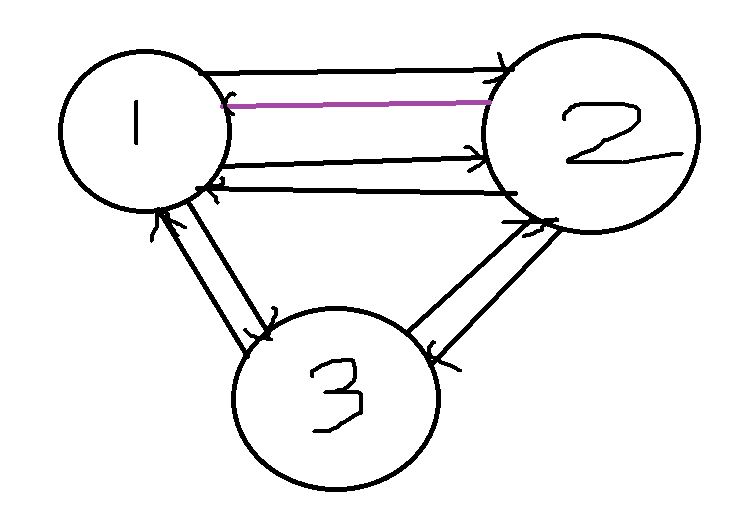
找到环之后要 continue 而不是直接return ,因为你可能两个骑士互相憎恨,这两个点就成了一个环,
-
然后又连接了其他的点,这样你就会 (MLE)
具体图例长这样:
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define LL long long
const int N = 1e6+10;
int n,m,tot = 1,x,st,en,id;
int head[N],w[N];
LL f[N][2],ans,maxn;
bool vis[N];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
struct node
{
int to,net;
}e[N<<1];
void add(int x,int y)
{
e[++tot].to = y;
e[tot].net = head[x];
head[x] = tot;
}
void find(int x,int from)//from 指从他来的编号
{
vis[x] = 1;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if((i ^ 1) == from) continue;//他不能是连向他父亲的边
if(vis[to])
{
st = x;//记录一下删除的边的编号以及这条边的左右端点
en = to;
id = i;
continue;//要把整棵树都搜完
// return;
}
else find(to,i);
}
}
void dp(int x,int from)//求最大独立集
{
f[x][1] = w[x]; f[x][0] = 0;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if((i ^ 1) == from || (i == (id ^ 1)) || i == id) continue;//他不可以是被删除的边,或者是返祖边
dp(to,i);
f[x][1] += f[to][0];
f[x][0] += max(f[to][1],f[to][0]);
}
}
int main()
{
n = read();
for(int i = 1; i <= n; i++)
{
w[i] = read(); x = read();
add(x,i); add(i,x);
}
for(int i = 1; i <= n; i++)
{
if(vis[i]) continue;//可能是基环树森林,要对每棵树都跑一边dp
// printf("-------->
");
find(i,0); maxn = 0;//找环
// cout<<st<<" "<<en<<" "<<id<<endl;
dp(st,0); //枚举两个端点的状态
maxn = max(maxn,f[st][0]);
dp(en,0);
maxn = max(maxn,f[en][0]);
ans += maxn;//加上每棵树的答案
}
printf("%lld
",ans);
return 0;
}