前言
点分治一般是用于解决树上路径问题。
前置知识
树的重心:把重心这个点割掉后,使所形成的最大的联通块大小最小的点。
可以证明重心子树的大小最大不会超过 (nover 2)
重心可以通过 (dfs) 一遍求出。
//maxsiz[x] 表示割掉点x后所形成的的最大的联通块的大小
void dfs(int x,int fa)
{
siz[x] = 1;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa) continue;
dfs(to,x);
siz[x] += siz[to];
max_siz[x] = max(max_siz[x],siz[to]);
}
max_siz[x] = max(max_siz[x],n-siz[x]);
if(max_siz[x] < max_siz[root]) root = x;
}
点分治
先来看到例题吧
给定一棵树和一个整数 (k),求树上边数等于 (k) 的路径有多少条
我们的暴力做法就是枚举每条两个点,然后在判断他们两个的距离是否为 (k)
大概是 O((n^3)) 的复杂度,优化一下的话可以跑到 O((n^2 log n))
这 (n) 的范围一大,还是会 (TLE), 考虑优化一下复杂度 。
我们现在主要想解决的是在以 (s) 为根的子树中符合条件的路径个数。
不难发现路径一共可以分为三类:
情况一
从 (s) 出发到他的子树中一个点 (t) 所形成的路径, 如图中的黄色路径:。
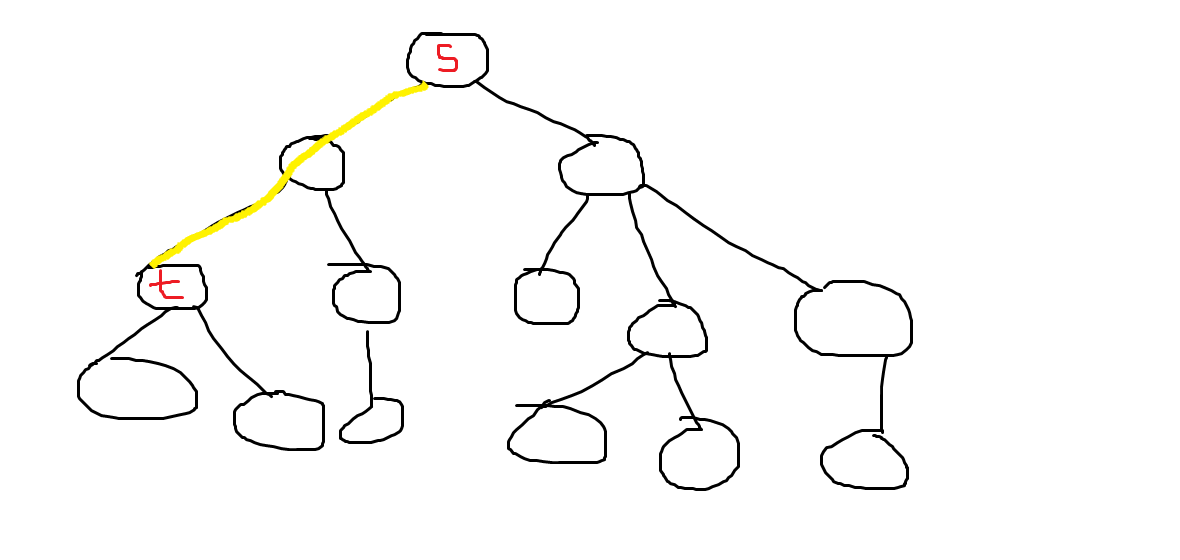
这个很好统计,可以直接由 (s) (dfs) 一遍即可, 复杂度 (O(m)) 。( (m) 为路径个数)
情况二:
不在 $s $ 的同一个子树中的两个点 (u,v) 所形成的路径,如图。

显然 (u-v) 的路径是肯定要经过点 (s) 的,那么 (u-v) 的路径也就可以拆成 (u-s) 和 (s-v) 的两条路径。
这两条路径我们在解决情况 (1) 的时候已经求出来了,剩下的就是考虑怎么把他们拼接起来。
设 (d_u) 表示 (u) 到 (s) 的距离,我们现在要解决的是 (d_u + d_v = k) 且 (u) 和 (v) 不在 (s) 的同一颗子树中的情况。
我们可以把 (d_u) 按从小到大排一下序,根据单调性,利用双指针就可以很好的解决这个问题。
但我们还要注意的是,需要排除两条在同一颗子树中的路径的干扰。
具体的做法就是对每一条路径记录他位于 (s) 的那一颗子树中。
这个可以和 (d_u) 一起在情况 (1) 的 (dfs) 中一并求出来。
假设路径条数为 (m) ,那么排序的复杂度为 (O(mlogm)), 双指针的复杂度为 (O(m)), 所以总的复杂度为 (O(mlogm))
那么第二种情况我们就解决出来了。
情况三:
位于 (s) 的同一颗子树中的 (u,v) 两点形成的路径,如图:

这个显然是当前问题的子问题,递归继续求解即可。
三种情况我们已经考虑完了,现在分析一下时间复杂度的问题。
假设递归的深度为 (k), 每做一次的复杂度最坏为 (O(nlogn)) (主要来自于情况2的排序)。
那么总的时间复杂度就是 (O(knlogn)), 所以为了保证复杂度,我们要使递归深度尽可能的小。
根据我们上面提到的关于重心的知识,每次分治的时候选取子树的重心,这样可以保证递归深度为 (logn)。
所以总的复杂度最坏为 (O(nlog^2n)) (实际上是很难达到这个上界的)
在做点分治的时候,我们需要把两个子树的信息合并,我们暴力合并的复杂度过高,有的情况下会使用启发式合并的方法来合并。
一般点分治的题套路都是一样的,都是分治递归求解,唯一的不同点就在于怎么合并子树的信息。
解决了合并子树信息这个问题,剩下的就是套模板的事情了。
例题代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e4+10;
int n,m,tot,cnt,sum_siz,root,u,v,w;
int head[N],siz[N],max_siz[N],dis[N],k[N];
bool vis[N],ans[N];
struct bian
{
int to,net,w;
}e[N<<1];
struct node
{
int d,wh;
node() {};
node(int x, int y){d = x; wh = y;}
}a[N];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s =s * 10+ch - '0'; ch = getchar();}
return s * w;
}
void add(int x,int y,int w)
{
e[++tot].w = w;
e[tot].to = y;
e[tot].net = head[x];
head[x] = tot;
}
bool comp(node a,node b)
{
return a.d < b.d;
}
void get_root(int x,int fa)//找重心
{
max_siz[x] = 0; siz[x] = 1;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa || vis[to]) continue;
get_root(to,x);
siz[x] += siz[to];
max_siz[x] = max(max_siz[x],siz[to]);
}
max_siz[x] = max(max_siz[x],sum_siz-siz[x]);
if(max_siz[x] < max_siz[root]) root = x;
}
void get_dis(int x,int fa,int who)//找到重心的距离, who 记录他是谁的子树
{
a[++cnt] = node(dis[x],who);
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa || vis[to]) continue;
dis[to] = dis[x] + e[i].w;
get_dis(to,x,who);
}
}
int search(int d)
{
int L = 1, R = cnt, res = 0;
while(L <= R)
{
int mid = (L+R)>>1;
if(a[mid].d >= d)
{
res = mid;
R = mid - 1;
}
else L = mid + 1;
}
return res;
}
void calc(int x,int d)
{
dis[x] = 0; cnt = 0;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(vis[to]) continue;
dis[to] = dis[x] + e[i].w;
get_dis(to,x,to);
}
a[++cnt] = node(0,0);
sort(a + 1, a + cnt + 1, comp);//排一下序
for(int i = 1; i <= m; i++)
{
if(ans[i]) continue;
int l = 1, r = cnt;
while(l <= cnt && a[l].d + a[r].d < k[i]) l++;
while(l <= cnt && !ans[i])
{
if(k[i] - a[l].d < a[l].d) break;
int id = search(k[i] - a[l].d);
while(a[id].d + a[l].d == k[i] && a[id].wh == a[l].wh) id++;
if(a[l].d + a[id].d == k[i]) ans[i] = 1;
l++;
}
}
}
void slove(int x)
{
calc(x,0); vis[x] = 1;//先算 x 点的贡献
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(vis[to]) continue;
max_siz[0] = n; sum_siz = siz[to]; root = 0;
get_root(to,0); slove(root);//递归处理子树
}
}
int main()
{
n = read(); m = read();
for(int i = 1; i <= n-1; i++)
{
u = read(); v = read(); w = read();
add(u,v,w); add(v,u,w);
}
for(int i = 1; i <= m; i++) k[i] = read();
max_siz[0] = sum_siz = n; root = 0;
get_root(1,0); slove(root);//找到一开始整颗树的重心
for(int i = 1; i <= m; i++)
{
if(ans[i]) puts("AYE");
else puts("NAY");
}
return 0;
}
例2: P4178 Tree
题目描述
给定一棵 (n) 个节点的树,每条边有边权,求出树上两点距离小于等于 (k) 的点对数量。
和模板题差不多,只要在合并子树的时候稍微改一下即可。
code:
#pragma GCC optimize(2)
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 4e4+10;
int n,m,tot,cnt,root,sum_siz,u,v,w,k,ans;
int head[N],siz[N],max_siz[N],dis[N],a[100010];
bool vis[N];
struct node
{
int to,net,w;
}e[N<<1];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s =s * 10+ch - '0'; ch = getchar();}
return s * w;
}
void add(int x,int y,int w)
{
e[++tot].w = w;
e[tot].to = y;
e[tot].net = head[x];
head[x] = tot;
}
void get_root(int x,int fa)
{
max_siz[x] = 0; siz[x] = 1;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa || vis[to]) continue;
get_root(to,x);
siz[x] += siz[to];
max_siz[x] = max(max_siz[x],siz[to]);
}
max_siz[x] = max(max_siz[x],sum_siz-siz[x]);
if(max_siz[x] < max_siz[root]) root = x;
}
void get_dis(int x,int fa)
{
a[++cnt] = dis[x];
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa || vis[to]) continue;
dis[to] = dis[x] + e[i].w;
get_dis(to,x);
}
}
int calc(int x,int d)
{
int res = 0;
dis[x] = d; cnt = 0;
a[++cnt] = dis[x];
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(vis[to]) continue;
dis[to] = dis[x] + e[i].w;
get_dis(to,x);
}
sort(a+1,a+cnt+1);
int L = 1, R = cnt;
while(L <= R)
{
if(a[L] + a[R] <= k)
{
res += R-L;
L++;
}
else R--;
}
return res;
}
void slove(int x)
{
ans += calc(x,0);
vis[x] = 1;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(vis[to]) continue;
ans -= calc(to,e[i].w);
max_siz[0] = n; sum_siz = siz[to]; root = 0;
get_root(to,0); slove(root);
}
}
int main()
{
n = read();
for(int i = 1; i <= n-1; i++)
{
u = read(); v = read(); w = read();
add(u,v,w); add(v,u,w);
}
k = read();
max_siz[0] = sum_siz = n; root = 0;
get_root(1,0); slove(root);
printf("%d
",ans);
return 0;
}
动态点分治
动态点分治又叫点分树(个人觉得点分树更形象一些),主要解决的树上的一下带修改问题。
动态点分治还是基于点分治的那套理论,每次选重心分治。
但考虑到修改操作,我们不可能每次修改都做一遍。
我们可以建点分树来解决这个问题,具体来说就是:
设当前的分治中心为 (x), 由他子树中的重心 (y) 向 (x) 连边,不难发现这样会构成一棵树,这棵树也被叫做点分树。
不难发现当我们要修改 (x) 这个节点的信息的时候,发现他会影响到的是 (x) 到根节点路径上的点的信息。
查询的话同样会用到 (x) 到根节点路径上点的信息。
由于我们树的高度不超过 (logn), 所以直接暴力修改查询即可。
我们就可以拿数据结构来维护每个点的信息,巴拉巴拉。
代码,咕咕咕