文章迁移说明:此文已由lightinglei于2019-02-18发布,是本人的另外一个账号,现同步迁移至本账号
一、正规方程、梯度下降原理介绍
正规方程:
先了解下线性模型,假设我们依据消费者的年龄、性别、职业3个特征来判断是否会进行购物消费,令x1代表年龄、x2代表性别、x3代表职业,则我们可以引入一个预测函数来判断是否会进行消费:f(x)=w1x1+w2x2+w3+w3x3+b,将其转化为向量的形式为:
![]() (公式一),其中w=(w1,w2,w3), b为常数
(公式一),其中w=(w1,w2,w3), b为常数
假设真实值为y取值为0或1,0代表不会消费,1代表会消费;
如果我们能与预测值f(x)无限接近这真实值y的一组w和b,那就可以进行判断了,如何判断两者的误差呢,这个时候需要引入均方误差了,我们的目的就是让均方误差最小化了,我们先考虑一种简单的情形,假设只有一个特征的情况,则均方误差函数为:
![]() (公式二),其中m为样本的个数
(公式二),其中m为样本的个数
求解w和b,相当于是求解H(w,b)的最小化过程,求解步骤如下:
(1)分别令该函数对w和b进行求导,则可得到关于w和b的两个等式
(2)分别令两个等式等于0,则可求得w和b
如果假设数据集为D,3个特征的情况,则我们叫做“多元线性回归问题”,解决该问题的步骤如下:
(1)令![]() 为特征参数
为特征参数
(2)将数据集D表示为一个m*(d+1) 的矩阵,这里m为样本个数,d=3为特征数,其矩阵表示如下:
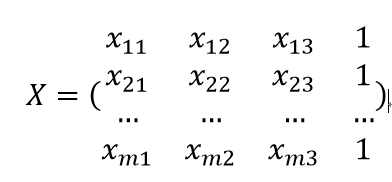
(3)令Y=(y1,y2,...ym)
则类比公式二,然后对![]() 进行求导,令等式等于0,则可推到出特征参数的表达式:
进行求导,令等式等于0,则可推到出特征参数的表达式:
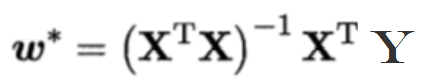 (公式三)
(公式三)
从整个的求解或推导的过程中,可以看到一次计算即可得出,不需要考虑学习率的问题,但是需要计算矩阵的转置和逆,因此当样本数量或特征参数很大时,计算花销较大,因此在实际解决问题中,该算法用的较少
梯度下降:
 (a表示步长,a后的等式可以理解为下降的方向)
(a表示步长,a后的等式可以理解为下降的方向)
由公式看起来比较晦涩,图形比较直观

从图像可以看出来,梯度下降算法是迭代进行的,沿着梯度下降的方向找到全局或局部的最优解,而每次迭代的步长由a决定,若a设置的太小,则需要多次才能找到最优解,若a设置的太大,则可能跳过最优解,从求解的过程中可以看出梯度下降需要设置步长学习率a,多次迭代进行寻求最优解,当特征数量较多时,也能取得较好的效果,因此应用较多。
二、正规方程、梯度下降实践
一下为利用正规方程和梯度下降求解sklearn中波士顿房价问题
"""
author:lightinglei
一、正规方程和梯度下降方法求解波士顿房价问题
y=w1x1+w2x2+w3x3+...wnxn+b,其中[x1,x2,x3...,xn]为特征,y为目标值,b为偏置,
[w1,w2,w3,...,wn]为权重系数组
正规方程:一步到位,缺点:不适合特征数很多的情况,因为求逆计算量大,时间长
梯度下降:多次迭代,往极值的方向进行下降
1)优点:高效、容易实现
2)缺点:SGD需要许多超参数,比如迭代数、正则项参数;对于特征标准化是敏感的
适用场景:如果数据量少于10万条则不推荐使用梯度下降,若超过10万条则推荐使用梯度下降(SGD)
"""
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error #mean_squared_error; 均方误差
from sklearn.externals import joblib
def Linear1_demo(): #正规方程
# 1.获取数据集
bostonData=load_boston()
print("特征数目:",bostonData.data.shape)
# 2.划分数据集
x_train,x_test,y_train,y_test=train_test_split(bostonData.data,bostonData.target,random_state=22)
# 3.特征工程:无量钢化处理-标准化
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)
# 4.预估器流程
estimator=LinearRegression()
estimator.fit(x_train,y_train)
print("正规方程最优的偏置为:",estimator.intercept_)
print("最优的权重系数为:",estimator.coef_)
# 5.模型评估
predict_y=estimator.predict(x_test)
error=mean_squared_error(y_test,predict_y)
print("正规方程均方误差为:",error)
return None
def Linear2_SGD_demo(): #梯度下降
# 1.获取数据集
bostonData=load_boston()
# 2.划分数据集
x_train,x_test,y_train,y_test=train_test_split(bostonData.data,bostonData.target,random_state=22)
# 3.特征工程:无量钢化处理-标准化
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)
# 4.预估器流程
estimator=SGDRegressor(learning_rate="constant",eta0=0.01,max_iter=10000)
estimator.fit(x_train,y_train)
print("梯度下降最优的偏置为:",estimator.intercept_)
print("梯度下降最优的权重系数为:",estimator.coef_)
# 5.模型评估
predict_y = estimator.predict(x_test)
error = mean_squared_error(y_test, predict_y)
print("梯度下降均方误差为:", error)
return None
if __name__=="__main__":
print("正规方程:
")
Linear1_demo()
print("梯度下降:
")
Linear2_SGD_demo()
""" 结果如下: 正规方程: 特征数目: (506, 13) 正规方程最优的偏置为: 22.62137203166228 最优的权重系数为: [-0.64817766 1.14673408 -0.05949444 0.74216553 -1.95515269 2.70902585 -0.07737374 -3.29889391 2.50267196 -1.85679269 -1.75044624 0.87341624 -3.91336869] 正规方程均方误差为: 20.627513763095404 梯度下降: D:Program Filespycharmprojectvenvlibsite-packagessklearnlinear_modelstochastic_gradient.py:183: FutureWarning: max_iter and tol parameters have been added in SGDRegressor in 0.19. If max_iter is set but tol is left unset, the default value for tol in 0.19 and 0.20 will be None (which is equivalent to -infinity, so it has no effect) but will change in 0.21 to 1e-3. Specify tol to silence this warning. FutureWarning) 梯度下降最优的偏置为: [22.64154175] 梯度下降最优的权重系数为: [-0.74660669 1.15751377 -0.04718662 0.56440515 -1.74582607 3.17916205 -0.03211535 -3.63628395 2.93605424 -1.56189505 -1.64378546 0.918139 -4.25393773] 梯度下降均方误差为: 22.980989639657214 """