一、梯度下降、随机梯度下降、批量梯度下降
- 梯度下降:梯度下降中,对于θ 的更新,所有的样本都有贡献,也就是参与调整θ 。其计算得到的是一个标准梯度。因而理论上来说一次更新的幅度是比较大的。如果样本不多的情况下,当然是这样收敛的速度会更快。
-
随机梯度下降:随机梯度下降法,随机用样本中的一个例子来近似总体样本,来调整θ 。所以随机梯度下降是会带来一定的问题,因为计算得到的并不是准确的全局的梯度,容易陷入到局部最优解中
-
批量梯度下降:批量的梯度下降就是一种折中的方法,他用了一些小样本来近似全部的,其本质就是一个样本不太准,那就用30或50个样本。那比随机的要准不少,而且批量的话还是非常能够准确反映总体样本的一个分布情况的。
二、公式推导
模型函数:
hθ(x)=Θx2+1
代价函数:
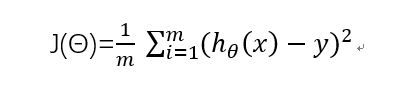
求导:
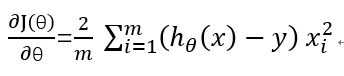
更新theta:
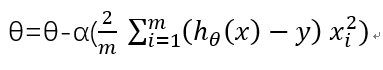
三、代码实例
说明:本例中假设空间为上述模型函数hθ(x),通过三个简单样本(1,2),(2,5),(3,10)求解参数θ的最优值,来对比分析梯度下降法。我们自己计算能提前得知该θ的最优解为θ=1。
1)同样的数据,迭代一次,分别进行单个梯度下降与批量梯度下降,结果会一样吗?
x=[1,2,3] y=[2,5,10] theta=5 step_size=0.01
单个梯度下降求解
for i in range(3):
pred_y=theta*x[i]**2+1
theta=theta-step_size*2*(pred_y-y[i])*x[i]**2
print("theta=",theta)
theta= 4.92
theta= 3.6656
theta= -0.6526720000000004
梯度下降法求解
pred_y=[]
for i in range(3):
pred_y.append(theta*x[i]**2+1)
pred_y=np.array(pred_y)
y=np.array(y)
theta=theta-step_size*2/3*np.dot((pred_y-y),np.square(x))
print("theta=",theta)
theta= 2.38666666667
2)进行多次迭代,随机梯度与梯度下降法效果如何呢?
import numpy as np
import random
x=[1,2,3]
y=[2,5,10]
theta=5
step_size=0.01
max_iters = 20
iter_count = 0
随机梯度下降多次迭代求解
while iter_count<max_iters:
i = random.randint(0,2)
pred_y=theta*x[i]**2+1
theta=theta-step_size*2*(pred_y-y[i])*x[i]**2
iter_count+=1
print("iter_count=%d,theta=%f"%(iter_count,theta))
iter_count=1,theta=3.720000 iter_count=2,theta=-0.686400 iter_count=3,theta=-0.146752 iter_count=4,theta=-0.123817 iter_count=5,theta=1.696767 iter_count=6,theta=1.682831 iter_count=7,theta=1.464325 iter_count=8,theta=1.455039 iter_count=9,theta=1.309426 iter_count=10,theta=1.303238 iter_count=11,theta=1.206202 iter_count=12,theta=0.872155 iter_count=13,theta=0.913065 iter_count=14,theta=0.914804 iter_count=15,theta=0.942067 iter_count=16,theta=1.035919 iter_count=17,theta=0.977730 iter_count=18,theta=0.978176 iter_count=19,theta=1.013531 iter_count=20,theta=1.013260
梯度下降多次迭代求解
while iter_count<max_iters:
pred_y=[]
for i in range(3):
pred_y.append(theta*x[i]**2+1)
pred_y=np.array(pred_y)
y=np.array(y)
theta=theta-step_size*2/3*np.dot((pred_y-y),np.square(x))
iter_count+=1
print("iter_count=%d,theta=%f"%(iter_count,theta))
iter_count=1,theta=2.386667
iter_count=2,theta=1.480711
iter_count=3,theta=1.166647
iter_count=4,theta=1.057771
iter_count=5,theta=1.020027
iter_count=6,theta=1.006943
iter_count=7,theta=1.002407
iter_count=8,theta=1.000834
iter_count=9,theta=1.000289
iter_count=10,theta=1.000100
iter_count=11,theta=1.000035
iter_count=12,theta=1.000012
iter_count=13,theta=1.000004
iter_count=14,theta=1.000001
iter_count=15,theta=1.000001
iter_count=16,theta=1.000000
iter_count=17,theta=1.000000
iter_count=18,theta=1.000000
iter_count=19,theta=1.000000
iter_count=20,theta=1.000000
四、总结
从上述实验结果可以看出,随机梯度与梯度下降法每次迭代都是沿着最陡的方向(也就是梯度的方向)前进。但是批梯度下降和随机梯度下降的所谓最陡的方向(梯度)是不一样的,批梯度下降所找到的方向是当前点,对于所有的样本所产生的Cost最陡的方向;而随机梯度下降所找到的方向是当前点对于这一次所选取的样本所产生的Cost_sgd 最陡的方向。由于这两个方法中的样本个数以及具体取值的不同,产生的梯度方向也不同,所以批梯度下降是一直朝着全局最陡的方向走的,而随机梯度下降的方向,会因为所选取的样本的具体不同而不同,从而在整体方向上会显得左右摇摆。上述实验2也契合了这个结论,随机梯度下降法出现了左右摇摆的情况,而梯度下降法总是稳定的向全局最优解一步步靠近。
在样本少的情况下,梯度下降法明显要收敛的更快一些,上述例子也看到了在进行到第8次迭代的时候,梯度下降法已经几乎接近收敛了;而随机梯度在20次才接近收敛。在训练样本多的情况下,sgd比gd的收敛速度快,一个原因是gd要通过所有样本计算梯度,而sgd通过一个样本计算一个近似的梯度,本身计算量就会小非常多,如果考虑到gd计算时有可能不是所有的样本都能到内存中,速度就会减少得更慢。
从收敛精度角度看,随机梯度收敛的是一个近似的精度,不如梯度下降法收敛精度准确,上述实验也再次佐证了这一点。幸运的是在机器学习中,我们有时候并不需要在训练集上得到一个非常精确的最优解,很多时候甚至需要early stop,近似最优解,也能解决实际问题。
最后,我们再次得出结论,mini-batch梯度下降法应该是一个不错的选择,既考虑到了收敛速度也保证了精确度。