快速幂算法——可迅速求出a^b。其主要理论依据如下:
1,当b为偶数时,a^b可以转为a^2的b/2次方。
2,当b为奇数时,a^b可以转为a^2的b/2次方,再乘以a。
//简单来说就是把b当成2进制形式,然后累加;
// 2*7=2*(1*2^0+1*2^1+1*2^2)=2*1*2^0+2*1*2^1+2*1*2^2;
//快速幂——加法
//简单来说就是把b当成2进制形式,然后累加;
// 7 = 111
// 2*7=2*(1*2^0+1*2^1+1*2^2)=2*1*2^0+2*1*2^1+2*1*2^2;
// = 2*1 + 2*2 + 2*4
// = 2 + 4 +8
// = 6 + 8
// = 14
// 2*(1*2^0) = 2
// 2*(1*2^1) = 4
// 2 * (1*2^2) = 8
代码:
long long cul_sum(long a, long b) { long ans = 0; while (b) { cout << "-------------" << endl; if (b & 1) { ans = ans + a;//将每一项的值加起来 合并最后的结果 cout << "ans = " << ans << endl; } a = a + a; //计算每一项的值 b >>= 1; cout << "a = " << a << endl; } return ans; } int main() { long a, b; cin >> a >> b; cout<<cul_sum(a, b) << endl; return 0; }
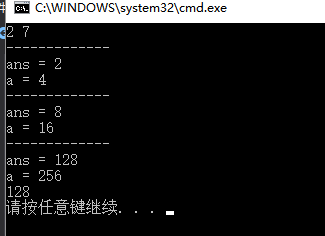
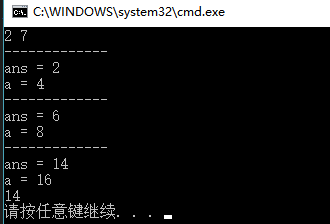
计算结果如下:
快速幂——乘方
、//快速幂——乘方 //简单来说就是把b当成2进制形式,然后累乘; // 7 = 111 // 2*7=2^(1*2^0+1*2^1+1*2^2)=2^(1*2^0) * 2^(1*2^1) * 2^(1*2^2); // = 2^1 * 2^2 * 2^4 // = 2 * 4 * 16 // = 8 * 16 // = 128 #include<iostream> using namespace std; long long cul_multi(long a, long b) { long ans = 1; while (b) { cout << "-------------" << endl; if (b & 1) { ans = ans * a; cout << "ans = " << ans << endl; } a = a * a; cout << "a = " << a << endl; b >>= 1; } return ans; } int main() { long a, b; cin >> a >> b; cout<<cul_multi(a, b) << endl; return 0; }