层次分析法量化用户的产品偏好

用户对产品有非常多行为，怎样进行用户行为分析来量化用户对产品的喜好程度呢？

比方豆瓣FM。用户能够点击“喜好”和"扔进垃圾箱"等；比方优酷视频，用户能够顶，踩，分享等。

我们怎样通过这些行为信息分析用户对这首歌的喜好程度，对这个视频的评分是多少。

以下实例分析用户对视频的喜好程度。说到视频，我们能够联想到各种用户行为。看了多久，是否评论。是顶是踩。是否分享？

我们能够通过这些指标来评估用户对该视频的打分。比方用户看了多久打多少分，分享了打多少分等。还有就是不同的行为也反映了不同程度的喜好。

我们能够通过一条简单的公司来评估打分。score=w1*x1+w2*x2.......

x1,x2等是行为指标，w1,w2等是行为权重。

行为指标：比方用户点了赞，给1分，分享了，给2分。

通常这里须要做归一化处理，把分数压缩到一个合理范围。

（PS：这里相当于领域专家打分，不知道是否通过建模的方法，有待探讨）。

行为权重：不同的行为，反映了用户的不同喜好程度，比方分享了比顶赞更重要。

面对众多指标，怎样合理地确定各权重呢？

这里通过层次分析法来确定各行为指标的权重。

构造成对照较矩阵

	播放时长	播放时长/ 视频时长	评论	下载	收藏	分享
播放时长	1	1/3	1	1/3	1/5	1/5
播放时长/ 视频时长	3	1	1	1	1	1/2
评论	1	1	1	1/3	1/2	1/5
下载	3	1	3	1	1	1/2
收藏	5	1	2	1	1	1/2
分享	5	2	5	2	2	1

比方第四行第一列的数字3，表示“下载”比“播放时长”稍重要。

标度	含义
1	表示两个元素相比，具有相同重要性
3	表示两个元素相比，前者比后者稍重要
5	表示两个元素相比。前者比后者明显重要
7	表示两个元素相比，前者比后者强烈重要
9	表示两个元素相比。前者比后者极端重要
2，4。6，8	表示上述相邻推断的中间值
倒数	若元素与的重要性之比为，那么元素与元素重要性之比为

列进行归一化

[[ 0.05555556 0.0521327 0.07692308 0.05830389 0.03508772 0.06896552]

[0.16666667 0.15797788 0.07692308 0.17667845 0.1754386 0.17241379]

[0.05555556 0.15797788 0.07692308 0.05830389 0.0877193 0.06896552]

[0.16666667 0.15797788 0.23076923 0.17667845 0.1754386 0.17241379]

[0.27777778 0.15797788 0.15384615 0.17667845 0.1754386 0.17241379]

[0.27777778 0.31595577 0.38461538 0.35335689 0.35087719 0.34482759]]

行求和

[ 0.34696846 0.92609846 0.50544522 1.07994462 1.11413265 2.0274106 ]

再归一化：

[ 0.05782808 0.15434974 0.08424087 0.17999077 0.18568877 0.33790177]

播放时长

播放时长/

视频时长

下载

0.05782808

0.15434974

0.08424087

0.17999077

0.18568877

0.33790177

就得到了个指标的权重

对于各项指标的得分，也要进行归一化处理，比方把分数限定在0-1.

假如一个用户对一个视频的各指标得分是

播放时长

播放时长/

视频时长

下载

0.9

0.8

1

0

则将得分进行加权求和（或者平均）。得到该用户对该视频的评分。

作一致性检验

从理论上分析得到：假设A是全然一致的成对照较矩阵，应该有

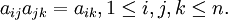
但实际上在构造成对照较矩阵时要求满足上述众多等式是不可能的。因此退而要求成对照较矩阵有一定的一致性，即能够同意成对照较矩阵存在一定程度的不一致性。

由分析可知。对全然一致的成对照较矩阵，其绝对值最大的特征值等于该矩阵的维数。

对成对照较矩阵的一致性要求，转化为要求：矩阵的绝对值最大的特征值和该矩阵的维数相差不大。

python代码实现

import numpy as np
import numpy.linalg as nplg
da = np.loadtxt("data.csv")
sum= np.sum(da,axis=0)
col_arv = da/sum
w = np.sum(col_arv,axis=1)
w_n = w/np.sum(w)
print w_n
print np.max(nplg.eig(da)[0])

输出是：

[ 0.05782808 0.15434974 0.08424087 0.17999077 0.18568877 0.33790177]
(6.16381602081+0j)

当中，第一行就是权重了，第二行就是最大特征值。

显然，矩阵的维数是6，跟最大特征值差点儿相同，合理。

PS:假设有什么更好的用户行为分析和量化用户产品偏好的做法，欢迎交流！

！

！！

！！。！！

！

參考资料：

http://wiki.mbalib.com/wiki/%E5%B1%82%E6%AC%A1%E5%88%86%E6%9E%90%E6%B3%95

http://courseware.ecnudec.com/zsb/zsx/zsx07/zsx07d/zsx07d000.htm