在上一篇文章中,我们简略介绍了与时间序列相关的应用,这次我们聚焦于时间序列的预测,讲讲与之相关的那些事。
1. 效果评估
设 y 是时间序列的真实值, yhat 是模型的预测值。在分类模型中由于y是离散的,有很多维度可以去刻画预测的效果。但现在的y是连续的,工具一下子就少了很多。时间序列里比较常用的是 MAPE(mean absolute percentage error) 和 RMSE (root mean square error)
个人比较喜欢MAPE,适合汇报,它揭示了预测值在真实值基础上的波动范围。比如,MAPE=10%,其代表着预测值的范围大致是 0.9y 至 1.1y
这两个指标或多或少都会有一些缺点,因此也有了各种变体,比如SMAPE, NRMSE等,感兴趣的可以自己去Wiki看看。
2. 交叉验证
因为时间序列的样本之间是无法交换的,所以没办法随机的像 KFold 一样把数据集切分成若干份训练集和测试集。但没关系,方法还是有的。
一个比较好的思路是按照时间顺序设置 cutoff time T_c :

这里有三个参数:
-
horizon: 模型预测的范围,如从cutoff点开始数未来30天
-
period: 每两个 cutoff 点之间的间隔,如60天
-
initial: 用于训练的日期范围,如730天
假设我们有2015-01-01 至 2017-12-31 共三年的数据。且三个参数的值如下: horizon=30,period=120,initial=730,则我们有
5组训练集和测试集。
有了交叉验证,我们就能获得评估模型效果和进行超参数优化了.
3. 时间序列预测模型
时间序列的预测有很多方法,本文不准备罗列的很细致,只展示三种模型:ARIMA,PROPHET,ETS,且都只用默认参数。在之后的一篇文章中,我会详细讲讲prophet的应用。
时间序列的预测模型,不好说一个模型绝对的好,跟数据集的类型有很大关系。根据更新的频率,可以分为Tick数据(小于1s,金融中的高频交易)、分钟数据、日数据、月数据等;根据波动情况,可以分为平稳序列和对日期/事件敏感的季节性序列等。一般数据的颗粒度越小,预测效果越差,因为随机性太大了,想通过模型来预测
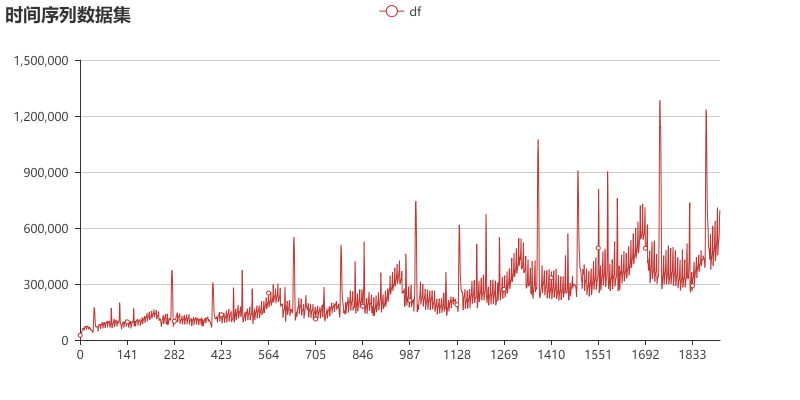
我找了一个对季节和节假日敏感的日数据来测试这几个模型,时间范围是5.3年。可以看到数据有一个整体的趋势,也有季节性趋势,还有那些尖峰对应的节假日/事件影响。
3.1 ARIMA 模型
在讲ARIMA模型之前得先熟悉ARMA模型(autoregressive moving average model)
ARMA 模型是经典的预测模型,有着成熟的理论基础,但条件也比较严格,就是要求时间序列是平稳的。这里讲的平稳性条件(一般指弱平稳)是指时间序列的均值与时间无关和方差仅与时间差有关。
在ARMA模型中,时序可以由如下方程表示:
其中 epsilon 是高斯白噪声序列。
可以从线性系统的角度去看ARMA 模型,已证明其是一个离散线性时不变系统,系统的输入是高斯白噪声序列(标准的平稳序列),输出是我们需要的时序y。此时上述式子可以写为
其中 L 是单位平移算子(lag operator).
有定理指出,对于一个离散线性平移不变系统而言,当输入是平稳序列时,可以证明输出也是平稳的,且输入序列和输出序列是平稳相关的。(这里面的东西还比较复杂,本科学的,现在已经忘了差不多了,感兴趣的同学可以自己去看看线性系统的理论)
商业中的数据大都不满足平稳性条件的,为了解决这个问题,所以就衍生了ARIMA 模型,中间的字母I代表的是差分。通过一些差分/季节性差分操作,我们能消除掉大部分趋势,使得原有不平稳的序列变得平稳(当然也不绝对,一般需要在差分后作平稳性检验)。
这里我设置交叉验证的参数如下:horizon,initial,period=30,1500,30 , 并生成12组训练集和测试集用来评估模型效果。
import pandas as pd
import numpy as np
from pyecharts import Bar
from pyecharts import Line
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline
from pyramid.arima import auto_arima
from fbprophet import Prophet
import ts_model_selection ##自己写的轮子,还没整理好,之后会放出来
df=pd.read_excel('.\data\tehr.xlsx')
df['ds']=pd.to_datetime(df['ds'])
df['logy']=np.log(df['y'])
horizon,initial,period=30,1500,30
df_train_list,df_test_list=ts_model_selection.train_test_split(
df,horizon='{} days'.format(horizon),initial='{} days'.format(initial),period='{} days'.format(period))
# 记录各个模型的分数
result={} #method,mape,cv
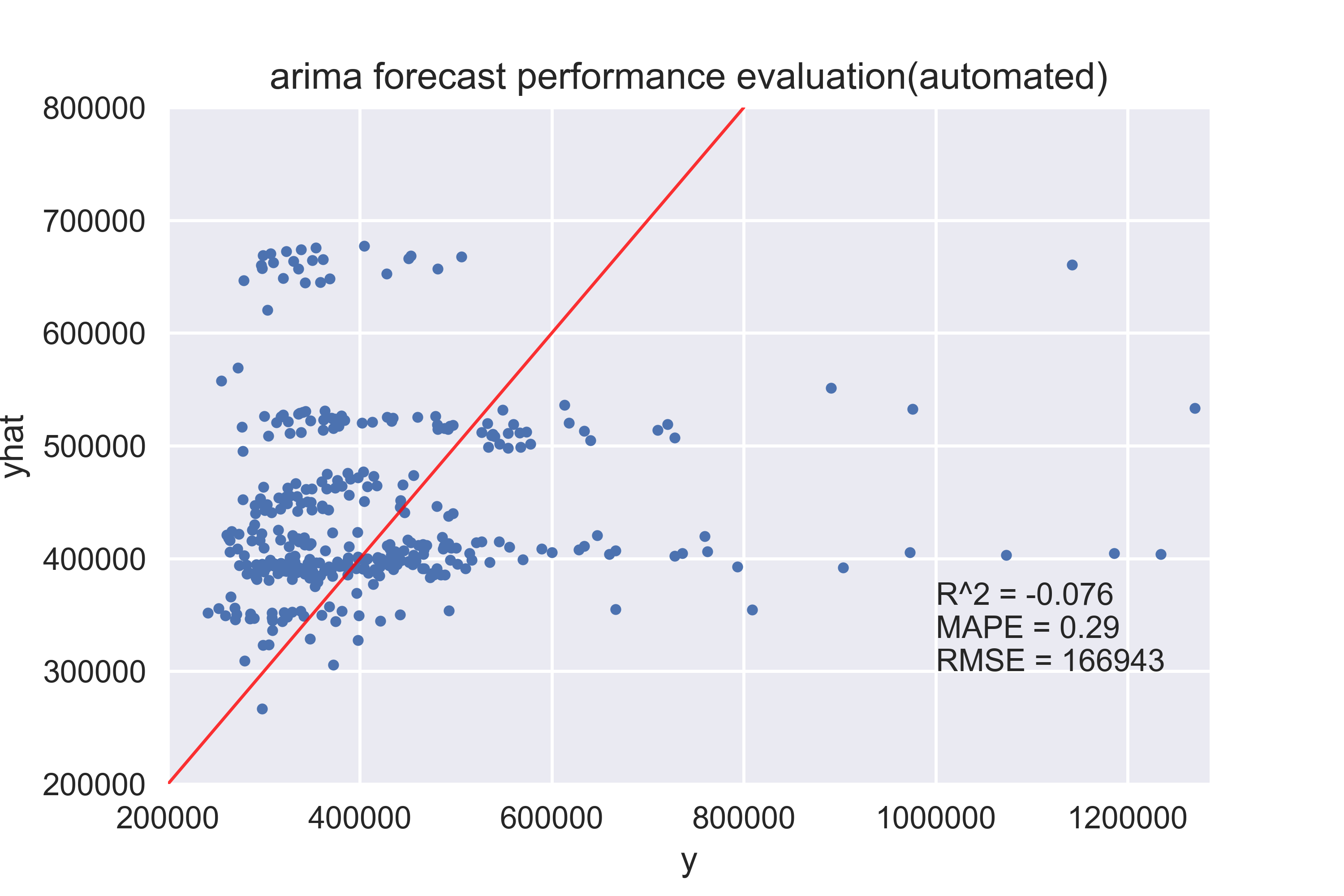
arima 有很多需要调参的地方,如p(AR),d(差分),q(MA)等。在 statsmodels 包中就有很多 ARIMA 相关的函数,但遗憾都需要手动调参。无奈找了一个仿照R中auto.arima写的包,还不错,名字是 pyramid-arima。接下来我们就用它来预测。
forecasts=pd.DataFrame(columns=['y','yhat','k'])
for k in range(len(df_train_list)):
#print(k)
df_train,df_test=df_train_list[k],df_test_list[k]
stepwise_fit = auto_arima(df_train['y'],seasonal=True,trace=False,error_action='ignore',suppress_warnings=True,stepwise=True)
yhat = stepwise_fit.predict(n_periods=horizon)
y=np.array(df_test['y'])
forecasts=pd.concat([forecasts,pd.DataFrame({'y':y,'yhat':yhat,'k':k})],axis=0)
result['auto.arima']={}
result['auto.arima']['mape']=np.mean(np.abs((forecasts['y']-forecasts['yhat'])/forecasts['y']))## 0.285
result['auto.arima']['rmse']=np.sqrt(np.sum((forecasts['y']-forecasts['yhat'])**2)/len(forecasts['y'])) ## 166943
print(result['auto.arima'])
forecasts_arima=forecasts.copy()#备份用
看了下,模型的MAPE是 0.285 ,RMSE 高达166943. 可能是由于数据过长,再加上没有调参,所以导致严重过拟合了。我也不打算深究了,感兴趣的可以细致的调一下。
3.2 Prophet 模型
facebook 在设计 prophet 之初,综合考虑了与时序预测相关的主要因素,具体包含:
- 季节性趋势,具体包含 yearly、weekly等
- 节假日和特殊事件的影响
- changepoint
- outlier
所以在商业上的应用场景会比较广,据说对于日数据的效果还不错。从大框架上讲,其是一个加法模型(经过log处理也可以变成一个乘法模型),一个时序会被分解为三部分之和
其中g(t)是趋势项, s(t) 是周期项,如 weekly 和 yearly 等,h(t)是节假日趋势
对于趋势项 g(t) 部分,可以由带changepoint的线性模型或者logistic growth (高中学的物种增长S型曲线?)模型来拟合:
其中 C 是carrying capacity,指明环境能容许的最大值,比如手机销售量最大也不会超过人口太多。k 是增长率。m是offset parameter。当加了changepoint 影响后,方程会有一些变化,具体可参见论文。
对于周期项 s(t) 部分,可以由Fourier series 来逼近
这里参数P的设置很有意思,facebook没有粗暴的直接用n,而是分别对yearly data,weekly data等作拟合。例如当P=7时, 序列 s(t) 的周期有 {7/n}
对于 节假日/事件 项 h(t) 部分,可以由示性函数来逼近
其中 D_i 是指节假日i的日期集合,Z(t) 是一个矩阵,kappa 是一个正态分布,拟合每一个节假日的影响程度
prophet 有很多参数可调,这里我们先都用默认的。
forecasts=pd.DataFrame(columns=['y','yhat','k'])
horizon,initial,period=30,1500,30
df_train_list,df_test_list=ts_model_selection.train_test_split(
df,horizon='{} days'.format(horizon),initial='{} days'.format(initial),period='{} days'.format(period))
for k in range(len(df_train_list)):
df_train,df_test=df_train_list[k],df_test_list[k]
m=Prophet()
m.fit(df_train[['ds','logy']].rename(columns={'logy':'y'}))
yhat=np.array(m.predict(df_test[['ds']])['yhat'])
y=np.array(df_test['logy'])
y,yhat=np.exp(y),np.exp(yhat)
forecasts=pd.concat([forecasts,pd.DataFrame({'y':y,'yhat':yhat,'k':k})],axis=0)
result['prophet']={}
result['prophet']['mape']=np.mean(np.abs((forecasts['y']-forecasts['yhat'])/forecasts['y'])) #平均MAPE ,0.126
result['prophet']['rmse']=np.sqrt(np.sum((forecasts['y']-forecasts['yhat'])**2)/len(forecasts['y'])) ##137291
print(result['prophet'])
forecasts_prophet=forecasts.copy()#备份用
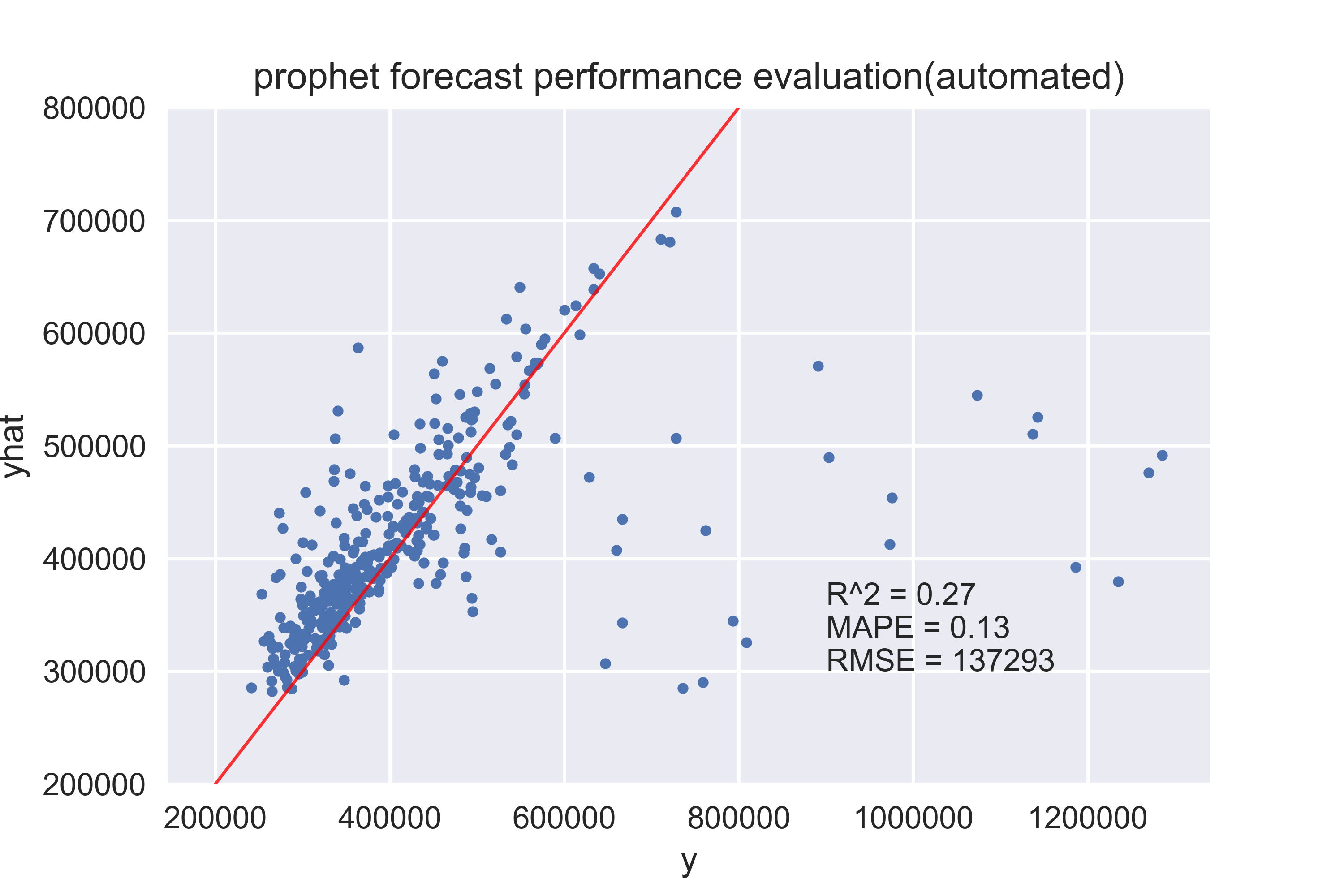
这里可以看到我把Y做了log化处理,这是因为log后,相当于把加法模型变成了乘法模型,对于我用的这份数据,乘法模型会更好一些。
可以看到模型的效果是 MAPE =0.13, RMSE=137293, 相比ARIMA要好很多了。
3.3 其他模型
除下上述两个,还有一些传统的可以用来预测时序的模型。本文就不再一一细讲,感兴趣的可以去看看R中的forecast包及其文档,介绍的很详细。
找了很久都没找到好的python包,所以这里提供一个在python中调用R中的ETS模型的code。
# 不保证这段代码能在任何环境中运行,需要大家自己去调
import os
os.environ['R_HOME'] = 'C:Program FilesRR-3.5.0'
os.environ['R_USER'] = 'C:Anaconda3Libsite-packages
py2'
import rpy2.robjects as robjects
from rpy2.robjects.packages import importr
ts=robjects.r('ts')
# import R's "base" package
base = importr('base')
# import R's "utils" package
utils = importr('utils')
forecast=importr('forecast',lib_loc = "C:/Users/gason/Documents/R/win-library/3.5")
from rpy2.robjects import pandas2ri
pandas2ri.activate()
df_train=df_train_list[1].loc[:,['y']]
rdata=ts(df_train)
horizon,initial,period=30,1500,30
df_train_list,df_test_list=ts_model_selection.train_test_split(
df,horizon='{} days'.format(horizon),initial='{} days'.format(initial),period='{} days'.format(period))
forecasts=pd.DataFrame(columns=['y','yhat','k'])
for k in range(len(df_train_list)):
#print(k)
df_train,df_test=df_train_list[k],df_test_list[k]
rdata=ts(df_train.loc[:,'y'])
yhat=forecast.forecast(forecast.ets(rdata),h=horizon)
yhat = np.asarray(yhat[1])
y=np.array(df_test['y'])
forecasts=pd.concat([forecasts,pd.DataFrame({'y':y,'yhat':yhat,'k':k})],axis=0)
result['ets']={}
result['ets']['mape']=np.mean(np.abs((forecasts['y']-forecasts['yhat'])/forecasts['y']))
result['ets']['rmse']=np.sqrt(np.sum((forecasts['y']-forecasts['yhat'])**2)/len(forecasts['y']))
print(result['ets'])
4. prphet 的调参
prophet 可调的参数有很多,个人比较比较调的有:
holidays: 需要注意的是,不是所有的节假日或时间都需要标记,以及windows的设置很考究;growth: 可选 linear 模型或者 logistic模型。个人意见,数据长度不长的话,直接用linear就好seasonality_prior_scale: 季节性趋势的强弱,默认为10holidays_prior_scale: 节假日趋势的强弱,默认为10changepoint_prior_scale:节changepoit的强弱,默认为0.05
对于分类模型,我们可以直接用sklearn的grid_search来调参,但对于时序,由于交叉验证的问题,我们没办法直接用。这里提供了一个函数供参考。
from fbprophet import Prophet
from fbprophet.diagnostics import cross_validation
from sklearn.model_selection import ParameterGrid
from sklearn.model_selection import ParameterSampler
def ts_evaluation(df,param,horizon=30,period=120,initial=1095,exp=True):
'''
利用交叉验证评估效果
'''
#param={'holidays':holidays,'growth':'linear','seasonality_prior_scale':50,'holidays_prior_scale':20}
m=Prophet(**param)
m.fit(df)
forecasts=m.predict(df[['ds']])
forecasts['y']=df['y']
df_cv = cross_validation(m, horizon='{} days'.format(horizon), period='{} days'.format(period), initial='{} days'.format(initial))
if exp:
df_cv['yhat']=np.exp(df_cv['yhat'])
df_cv['y']=np.exp(df_cv['y'])
mape=np.mean(np.abs((df_cv['y'] - df_cv['yhat']) / df_cv['y']))
rmse=np.sqrt(np.mean((df_cv['y'] - df_cv['yhat'])**2))
scores={'mape':mape,'rmse':rmse}
return scores
def ts_grid_search(df,holidays,param_grid=None,cv_param=None,RandomizedSearch=True,random_state=None):
'''网格搜索
时间序列需要特殊的交叉验证
df:
holidays: 需要实现调好
'''
df=df.copy()
if param_grid is None:
param_grid={'growth':['linear']
,'seasonality_prior_scale':np.round(np.logspace(0,2.2,10))
,'holidays_prior_scale':np.round(np.logspace(0,2.2,10))
,'changepoint_prior_scale':[0.005,0.01,0.02,0.03,0.05,0.008,0.10,0.13,0.16,0.2]
}
if RandomizedSearch:
param_list=list(ParameterSampler(param_grid,n_iter=10,random_state=random_state))
else:
param_list=list(ParameterGrid(param_grid))
if cv_param is None:
cv_param={'horizon':30,'period':120,'initial':1095}
scores=[]
for i,param in enumerate(param_list):
print('{}/{}:'.format(i,len(param_list)),param)
param.update({'holidays':holidays})
scores_tmp=ts_evaluation(df,param,exp=True,**cv_param)
param.pop('holidays')
tmp=param.copy()
tmp.update({'mape':scores_tmp['mape'],'rmse':scores_tmp['rmse']})
scores.append(tmp)
print('mape : {:.5f}%'.format(100*scores_tmp['mape']))
scores=pd.DataFrame(scores)
best_param_=scores.loc[scores['mape'].argmin(),:].to_dict()
best_scores_=best_param_['mape']
best_param_.pop('mape')
best_param_.pop('rmse')
return best_param_,best_scores_,scores
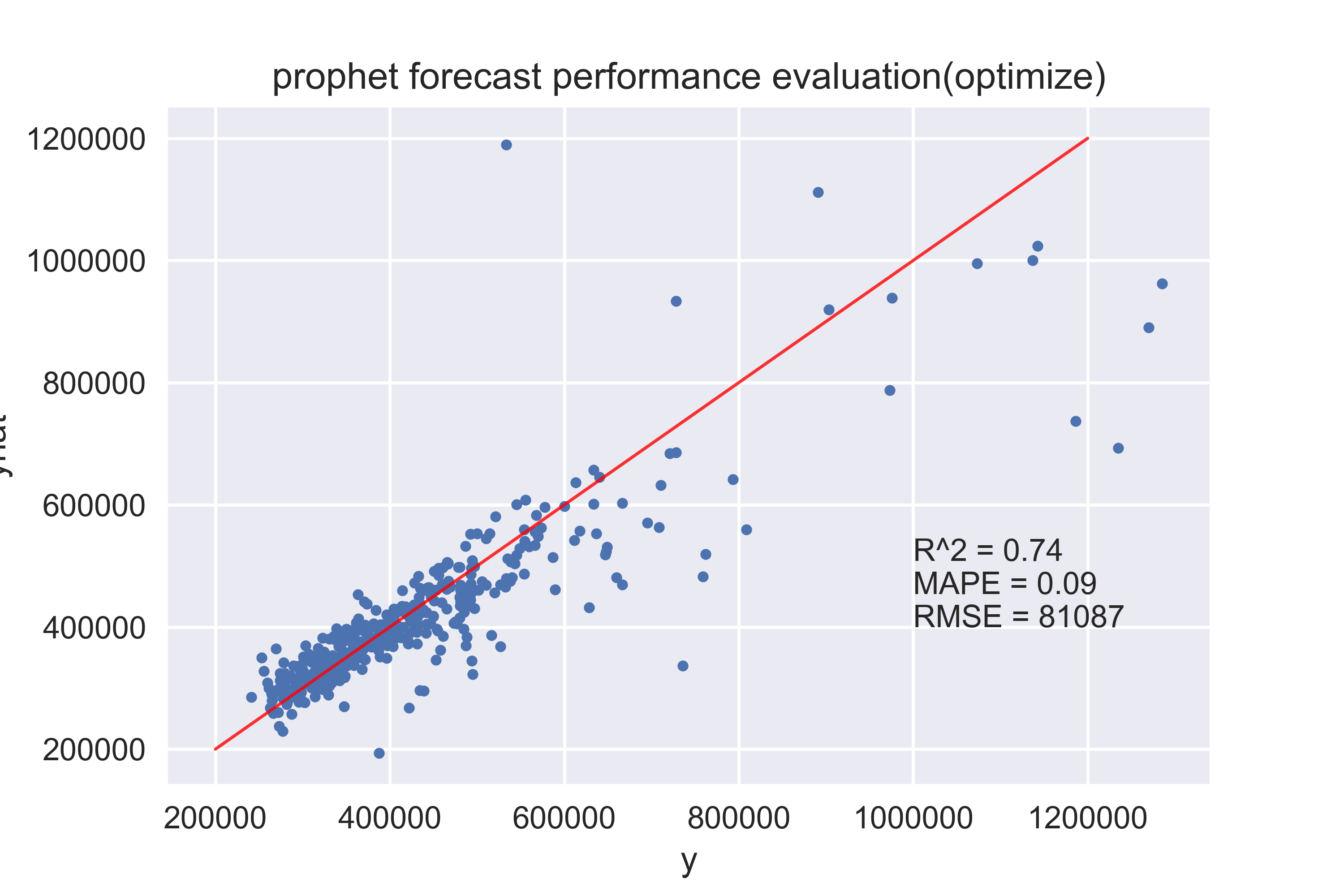
当然不是说上来直接暴力调参就好,我看了下,对于这份数据而言,changepoint_prior_scale 的影响最大,在一定范围内,越大效果越好。
下面附上我最后的效果。