序列最小最优化算法
前面我们讲过了支持向量机的原理,将我们的问题转化为约束优化问题,但还没有提到使用什么方法求解最优化解。
事实上一般我们用SMO(序列最小最优化算法)求解最优解,最要是这个算法即使在训练样本很大的时候,仍然可以有很快的收敛速度。
SMO算法需要求解的支持向量机对偶问题如下:

上式,我们需要求解的变量就是拉格朗日乘子,每一个变量
都对应一个样本
;只要求解出
每一个
就可以得到我们的模型。

SMO算法是一种启发式算法,其思路就是不断更新每一个拉格朗日乘子,使它们满足KKT条件,KKT条件与拉格朗日函数关系关系密切,来自于拉格朗日对偶函数求其最优解时,得来的结论,即如果原始问题与对偶问题若有相同的解,则他们的解需满足KKT条
件。
那么什么时候原始问题与对偶问题有相同的解?我在之前介绍拉朗日函数的时候提到过这个定理,感兴趣的可以看看,其实这个定理很好记,即不等式约束严格满足,等式约束是放射函数,则原始问题和对偶问题是有相同的解的。
https://blog.csdn.net/weixin_43327597/1article/details/104321889
关于KKT条件具体是什么这里就不介绍了,我准备在以后的博客里也专门写一篇介绍一下。
那么现在我来具体介绍一下SMO算法的思想,SMO算法,针对我们需要求解的约束优化问题,我们需要知道这几点
1.不断更新的意图是是最小化函数的值不断变小,以至于最后得到是最小化函数最小的最优解。
2.拉格朗日乘子最后需要满足KKT条件
所以SMO算法的思路是,从众多的拉格朗日乘子中选择两个,其余固定,之后不断更新这两个
的值,达到使优化函数最小的目的。达到收敛之后,再重复上述操作选择另外两个
进行收敛。所以按照上面的操作当选择两个拉格朗日乘子进行迭代时,其他的
则固定,所以约束优化问题变为下式

上式,i=1,2即为我们选择的那两个变量,其余则固定,选择的两个变量其中应至少有一个不满足KKT条件,则才有迭代的价值。当都满足KKT条件时,则说明最最优解已经求出。其中
下标为1,2的样本特征向量的核函数表示。
在这里其实有一个约束大家都能看到,k是一个常数,因为我们固定了其他的
,i=3,4,..N.所以初始化所有的
时需要满足

当 alpha _{1}-alpha _{2}=K, y_{1} = y_{2} doteq > alpha _{1}+alpha _{2}=K" class="mathcode" src="https://private.codecogs.com/gif.latex?y_%7B1%7D%20%5Cneq%20y_%7B2%7D%20%5Cdoteq%20%3E%20%5Calpha%20_%7B1%7D-%5Calpha%20_%7B2%7D%3DK%2C%20y_%7B1%7D%20%3D%20y_%7B2%7D%20%5Cdoteq%20%3E%20%5Calpha%20_%7B1%7D+%5Calpha%20_%7B2%7D%3DK">,所以我们需要在上述关系中找出最优的,事实上我们确定了
也就等于确定了
,且
的取值范围是可以确定的由上面不等式应该可以看出,这里不做描述了。那么我们如何迭代
呢?

即为样本被分类标记的真实值,g(Xi)为模型得到的预测值Ei为预测值与真实值之差
则更新公式为
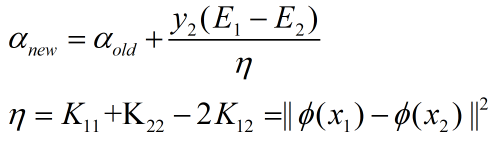
在核函数那一篇博客讲过,这里是一个非线性映射,将输入空间映射到特征空间,通过此公式求得其中一个
之后,再利用求出的
计算另一个。
那就讲到这里,上面可能有一个疑惑,最后两个公式怎么来的?其实是通过将两个变量用一个表示,然后求导得到的,这里就不多说了,很简单的数学原理,只是公式十分复杂。