一本通1654车的放置

1654：车的放置

时间限制: 1000 ms         内存限制: 524288 KB

【题目描述】

有下面这样的一个网格棋盘，a,b,c,d 表示了对应边长度，也就是对应格子数。

当 a=b=c=d=2 时，对应下面这样一个棋盘：

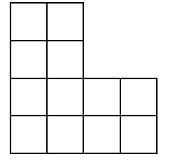
要在这个棋盘上放 k 个相互不攻击的车，也就是这 k 个车没有两个车在同一行，也没有两个车在同一列，问有多少种方案。同样只需要输出答案 mod10⁵+3 后的结果。

【输入】

第一行为有五个非负整数 a,b,c,d 和 k。

【输出】

包括一个正整数，为答案 mod10⁵+3 后的结果。

【输入样例】

2 2 2 2 2

【输出样例】

38

【提示】

数据范围与提示：

对于全部数据，1≤a,b,c,d,k≤1000，且保证了至少有一种可行方案。

sol：看上去较_水，实际上除了几个要特判的就没有了

把它看做两个矩形（看成三个容斥也行，但想到两个就不会写这个了吧）

一个a*b的矩形中，放 i 个方案数就是P(a,i)*C(b,i)或者P(b,i)*C(a,i)，

在下一个(a+c)*d矩形中，放 j 个的方案数就是P(a+c-i,j)*C(d,j)种方案数

O(k)枚举 i 即可

Ps：在C和P中要注意判断m和n的大小关系

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
    ll s=0;
    bool f=0;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-'); ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<3)+(s<<1)+(ch^48); ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<0)
    {
        putchar('-'); x=-x;
    }
    if(x<10)
    {
        putchar(x+'0');    return;
    }
    write(x/10);
    putchar((x%10)+'0');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('
')
const ll Mod=100003;
const int N=2005;
ll a,b,c,d,k;
ll Jiec[N],InvJiec[N];
inline ll Ksm(ll x,ll y)
{
    ll ans=1;
    while(y)
    {
        if(y&1) ans=ans*x%Mod;
        x=x*x%Mod;
        y>>=1;
    }
    return ans;
}
inline ll C(ll n,ll m)
{
    if(n<m) return 0;
    if(!InvJiec[m]) InvJiec[m]=Ksm(Jiec[m],Mod-2);
    if(!InvJiec[n-m]) InvJiec[n-m]=Ksm(Jiec[n-m],Mod-2);
    return Jiec[n]*InvJiec[m]%Mod*InvJiec[n-m]%Mod;
}
inline ll P(ll n,ll m)
{
    if(n<m) return 0;
    if(!InvJiec[n-m]) InvJiec[n-m]=Ksm(Jiec[n-m],Mod-2);
    return Jiec[n]*InvJiec[n-m]%Mod;
}
int main()
{
    ll i,ans=0;
    R(a); R(b); R(c); R(d); R(k);
    Jiec[0]=InvJiec[0]=1;
    for(i=1;i<=max(a+c,b+d);i++)
    {
        Jiec[i]=Jiec[i-1]*i%Mod;
    }
    for(i=0;i<=k;i++)
    {
        ll P1=i,P2=k-i;
        ll S1=P(a,P1)*C(b,P1)%Mod,S2=P(a+c-P1,P2)*C(d,P2)%Mod;
        ans+=S1*S2%Mod;
        ans-=(ans>=Mod)?Mod:0;
    }
    Wl(ans);
    return 0;
}
/*
input
2 2 2 2 2
output
38

input
4 2 2 4 4
output
3144

input
10 10 1 100 10
output
21223

input
555 666 777 888 999
output
94649
*/