1609:【例 4】Cats Transport
时间限制: 1000 ms 内存限制: 524288 KB

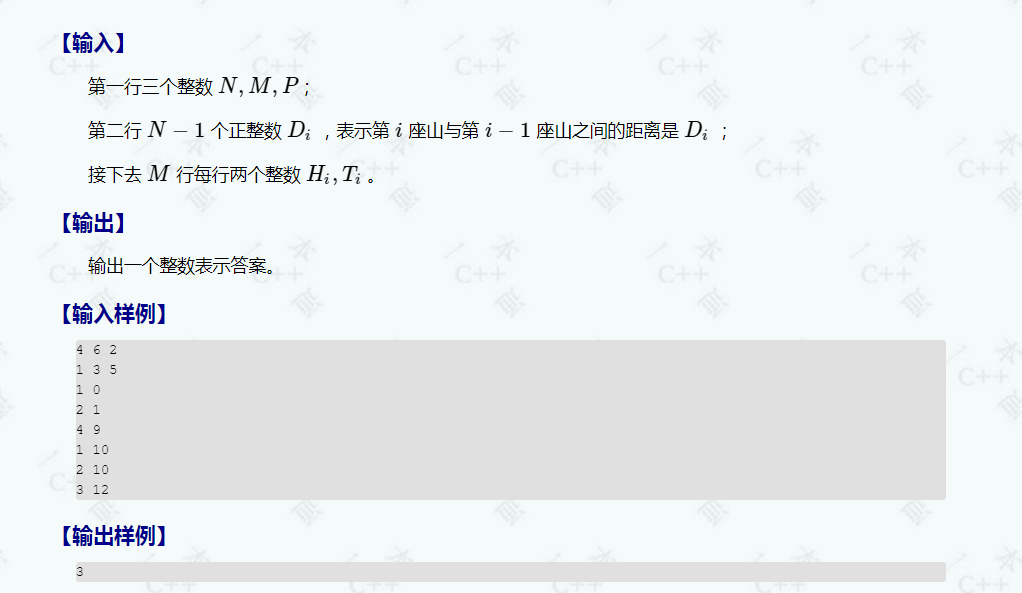
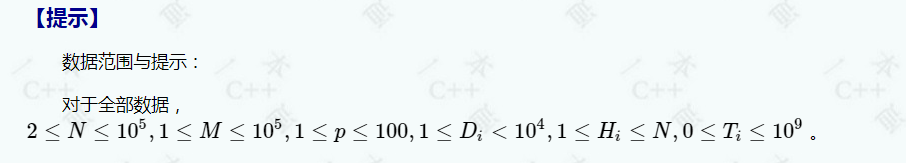
sol:非常偷懒的截图了事
注意:只能猫等人,不能人等猫
对于每只猫,我们可以得到一个数字 Cost[i] 表示Dis[H[i]]-T[i],表示在Cost[i]时刻出发刚好不用等(如果出发时间小于Cost[i],就会错过,反之则需要等待)
显然Cost需要排序
那么每个饲养员一定是掌管一段连续的Cost,直接dp是p*m2的,所以用斜率优化,非常套路
推出若 k<l<j
如果(dp_Last[l]+Qzh[l])-(dp_Last[k]+Qzh[k])<=(l-k)*Cost[j] 成立时 l 比 k 优

#include <bits/stdc++.h> using namespace std; typedef int ll; inline ll read() { ll s=0; bool f=0; char ch=' '; while(!isdigit(ch)) { f|=(ch=='-'); ch=getchar(); } while(isdigit(ch)) { s=(s<<3)+(s<<1)+(ch^48); ch=getchar(); } return (f)?(-s):(s); } #define R(x) x=read() inline void write(ll x) { if(x<0) { putchar('-'); x=-x; } if(x<10) { putchar(x+'0'); return; } write(x/10); putchar((x%10)+'0'); return; } #define W(x) write(x),putchar(' ') #define Wl(x) write(x),putchar(' ') const int N=100005,B=105; int n,m,P; int Dis[N]; int H[N],T[N],Cost[N],Qzh[N]; int dp[N][B]; int main() { int i,j,k; R(n); R(m); R(P); for(i=2;i<=n;i++) { Dis[i]=Dis[i-1]+read(); } for(i=1;i<=m;i++) { R(H[i]); R(T[i]); Cost[i]=T[i]-Dis[H[i]]; } sort(Cost+1,Cost+m+1); for(i=1;i<=m;i++) { Qzh[i]=Qzh[i-1]+Cost[i]; } memset(dp,63,sizeof dp); dp[0][0]=0; for(i=1;i<=m;i++) { for(j=1;j<=P;j++) { for(k=0;k<i;k++) { dp[i][j]=min(dp[i][j],dp[k][j-1]+Cost[i]*(i-k)-(Qzh[i]-Qzh[k])); } } } Wl(dp[m][P]); return 0; }

#include <bits/stdc++.h> using namespace std; typedef long long ll; inline ll read() { ll s=0; bool f=0; char ch=' '; while(!isdigit(ch)) { f|=(ch=='-'); ch=getchar(); } while(isdigit(ch)) { s=(s<<3)+(s<<1)+(ch^48); ch=getchar(); } return (f)?(-s):(s); } #define R(x) x=read() inline void write(ll x) { if(x<0) { putchar('-'); x=-x; } if(x<10) { putchar(x+'0'); return; } write(x/10); putchar((x%10)+'0'); return; } #define W(x) write(x),putchar(' ') #define Wl(x) write(x),putchar(' ') const int N=100005,B=105; int n,m,P; ll Dis[N]; ll H[N],T[N],Cost[N],Qzh[N]; ll dp[N],dp_Last[N]; int Que[N]; inline bool Panduan(int k,int l,int j) //k<l<j { ll S1=(dp_Last[l]+Qzh[l])-(dp_Last[k]+Qzh[k]); ll S2=(l-k)*Cost[j]; return (S1<=S2)?(1):0; } inline bool Panduan_Rev(int k,int l,int j) //k<l<j { ll S1=((dp_Last[l]+Qzh[l])-(dp_Last[k]+Qzh[k]))*(j-l); ll S2=((dp_Last[j]+Qzh[j])-(dp_Last[l]+Qzh[l]))*(l-k); return (S1>=S2)?(1):(0); } int main() { int i,j,k; R(n); R(m); R(P); for(i=2;i<=n;i++) { Dis[i]=Dis[i-1]+read(); } for(i=1;i<=m;i++) { R(H[i]); R(T[i]); Cost[i]=T[i]-Dis[H[i]]; } sort(Cost+1,Cost+m+1); for(i=1;i<=m;i++) { Qzh[i]=Qzh[i-1]+Cost[i]; dp[i]=Cost[i]*i-Qzh[i]; } for(i=2;i<=P;i++) { memmove(dp_Last,dp,sizeof dp); int Head=1,Tail=1; Que[1]=0; for(j=1;j<=m;j++) { while(Head<Tail&&Panduan(Que[Head],Que[Head+1],j)) Head++; int Pos=Que[Head]; dp[j]=dp_Last[Pos]+Cost[j]*(j-Pos)-(Qzh[j]-Qzh[Pos]); while(Head<Tail&&Panduan_Rev(Que[Tail-1],Que[Tail],j)) Tail--; Que[++Tail]=j; } } Wl(dp[m]); return 0; } /* input 4 6 2 1 3 5 1 0 2 1 4 9 1 10 2 10 3 12 output 3 */
