【转载请注明来自 Galaxies的博客:http://cnblogs.com/galaxies】
这篇文章当做一个记录啦qwq
参考:《K-D Tree在信息学竞赛中的应用》(n+e, 2016-07-31)
一棵二叉树(类似于BST二叉排序树)来维护一个k维空间。每个节点表示的是一个k维空间的区域。
每个节点还存储这一个具体的点,以它的某个坐标来划分出两个k维的空间,为这个节点的儿子所代表的区域。
我们姑且称这个具体的点为代表点。
啥意思呢?
struct node { int d[K], mx[K], mi[K], l, r; ... };
d[K]表示这个节点的代表点。这个节点存储的信息是一个K维空间:
第1维 [mi[0], mx[0]];第2维 [mi[1], mx[1]];...;第K维 [mi[K], mx[K]]
l和r存储的是按照代表点的某个坐标来进行划分的两个k维的空间。
为了使得区间平均,我们通常采用按照每个坐标轮流划分。
比如:平面,那么就是2维空间,依次按照 横、纵、横、纵、……划分
3维空间,依次按照 横、纵、高、横、纵、高、……划分
这样可以使得划分出来的空间尽量平均。
比如一个平面的划分方案如下,右图为对应的K-D Tree

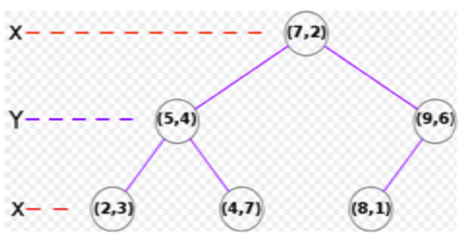
划分的过程中,我们需要找到一个代表点,这个代表点通常选取按用来划分的坐标排序的中位数这个点。
STL有一个方便的nth_element可以实现这个功能。
构造应该比较简单?不放代码啦。
然后是插入一个点。
从根往下比较,跟BST类似,就能找到插入的位置了。
下面是一个二维的示范,up里面可以维护信息,“。。。”里面就是把信息扔到K-D Tree的过程。
以下代码如果没有特别说明,ls为T[x].l;rs为T[x].r(预define了)
inline void insert(int &x, int d) { if(!x) { x = ++siz; T[x].d[0] = T[x].mi[0] = T[x].mx[0] = tmp.d[0]; T[x].d[1] = T[x].mi[1] = T[x].mx[1] = tmp.d[1]; } if(tmp == T[x]) { ... return ; } if(tmp.d[d] < T[x].d[d]) insert(ls, d^1); else insert(rs, d^1); up(x); }
然后你需要查询一个k维空间的值,就看是否完全包含/完全不包含
如果以上两类都可以直接回答。否则递归。
inline int query(int x, int x1, int y1, int x2, int y2) { if(!x) return 0; int ret = 0; if(in(x1, y1, x2, y2, T[x].mi[0], T[x].mi[1], T[x].mx[0], T[x].mx[1])) return ... if(out(x1, y1, x2, y2, T[x].mi[0], T[x].mi[1], T[x].mx[0], T[x].mx[1])) return 0; if(in(x1, y1, x2, y2, T[x].d[0], T[x].d[1], T[x].d[0], T[x].d[1])) ret += ...; ret += query(ls, x1, y1, x2, y2) + query(rs, x1, y1, x2, y2); return ret; }
上面是一个二维的例子,“。。。”里面可以自行维护需要的东西。
然后我们发现如果K-D Tree的一个区间被插入了好多次那么复杂度会退化(BST没有带平衡)
解决这个问题的办法有两个:
一个比较暴力,就是我的K-D Tree的节点个数达到阈值SIZE的整数倍的时候,就把K-D Tree的节点拎出来,重构K-D Tree即可。
阈值3000-10000(大概
这是一个二维的例子,t里存的是拎出来的旧节点。
inline int rebuild(int l, int r, int d) { if(l>r) return 0; int mid = l+r>>1; D = d; nth_element(t+l, t+mid, t+r+1); T[mid] = t[mid]; T[mid].l = rebuild(l, mid-1, d^1); T[mid].r = rebuild(mid+1, r, d^1); up(mid); return mid; }
还有一个办法,就是

这个复杂度是对的,就是写起来还要多维护一个size,我这么懒的人肯定是留着坑以后再说啊。。
(不过前面一个复杂度也是对的吧)
对于一些问题的估价:
比如我要询问(x,y)到平面上哪个点欧几里得距离最小啊之类的。
距离最小:一个点离当前域的最小距离(在域内为0)
距离最大:一个点离当前域的最大距离
常见估价:(可以理解)
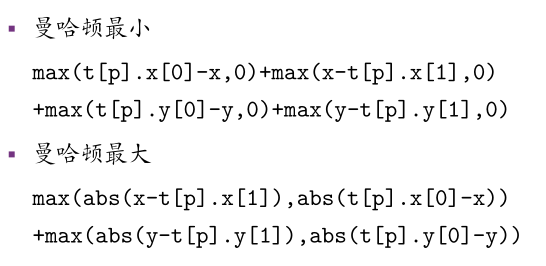

那么询问(x,y)离哪个点xx距离最小的话。。
就是看看估价,优先访问估价低的。如果最小可能距离都比当前答案大,就不用取管了。
复杂度O(logn)(随机),O(根号n)(构造)
kdtree估价例题:http://www.cnblogs.com/galaxies/p/bzoj2648.html
反正。。挺优秀的。
K-D Tree还可以代替很多类似什么三维偏序啊之类的为题
K维K-D Tree的查询复杂度约为O(n^(1-1/k))
那么可持久化树套树(三维空间的求值)就能在O(n^(5/3))的时间内求出来啊!
论写优秀暴力的重要性。
好了大概讲这么多(去睡觉啦qwq
有空再更