题目链接:
https://vjudge.net/problem/POJ-3565
题目大意:
在坐标系中有N只蚂蚁,N棵苹果树,给你蚂蚁和苹果树的坐标。让每只蚂蚁去一棵苹果树,
一棵苹果树对应一只蚂蚁。这样就有N条直线路线,问:怎样分配,才能使总路程和最小,且
N条线不相交。
解题思路:
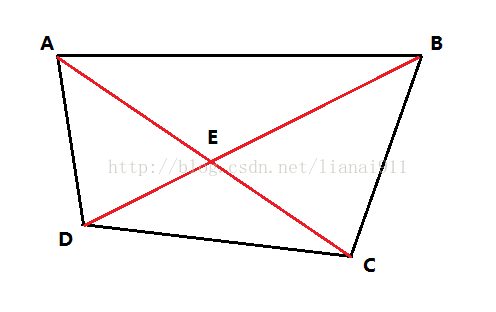
用一个图来说明思路。
假设A、B为蚂蚁,C、D为苹果树。则存在两种匹配:第一种是AD、BC,第二种是AC、BD。
根据三角形不等式AD+BC < AC+BD,最后得到很重要的一个性质——满足总路程之和最小
的方案一定不相交。现在来构建二分图,一边为蚂蚁,另一边为苹果树,以距离为边权值,题
目就变为了求带权二分图最小权和的最佳匹配。反向来思考,将距离乘以-1取负值建图,那么
就变为了求带权二分图最大权和的最佳匹配。直接用KM算法来做。
注意:用double,用slack数组优化(比全局变量快很多,网上看到说对于完全图优化会很快,用全局变量代替slack数组就超时)
1 #include<iostream> 2 #include<vector> 3 #include<cstring> 4 #include<queue> 5 #include<cmath> 6 #include<cstdio> 7 using namespace std; 8 const int maxn = 300 + 10; 9 const int INF = 0x3f3f3f3f; 10 double Map[maxn][maxn]; 11 double wx[maxn], wy[maxn];//顶标值 12 int cx[maxn], cy[maxn]; 13 //cx[i]表示与x部的点i匹配的y部的点的编号 14 //cy[i]表示与y部的点i匹配的x部的点的编号 15 bool visx[maxn], visy[maxn];//标记y部的点是否加入增广路 16 int cntx, cnty;//x部点的数目和y部点的数目 17 double minz;//边权顶标最小值 18 double slack[maxn]; 19 bool dfs(int u)//进入的都是X部的点 20 { 21 visx[u] = 1; 22 for(int v = 1; v <= cnty; v++) 23 { 24 if(!visy[v] && Map[u][v] != INF) 25 { 26 double t = wx[u] + wy[v] - Map[u][v]; 27 if(fabs(t) < 1e-5) 28 { 29 visy[v] = 1; 30 if(cy[v] == -1 || dfs(cy[v])) 31 { 32 cx[u] = v; 33 cy[v] = u; 34 return true; 35 } 36 } 37 else if(slack[v] > t) 38 slack[v] = t; 39 } 40 } 41 return false; 42 } 43 44 void KM() 45 { 46 memset(cx, -1, sizeof(cx)); 47 memset(cy, -1, sizeof(cy)); 48 memset(wy, 0, sizeof(wy)); 49 for(int i = 0; i <= cntx; i++)wx[i] = -1.0 * INF; 50 for(int i = 1; i <= cntx; i++) 51 { 52 for(int j = 1; j <= cnty; j++) 53 { 54 wx[i] = max(wx[i], Map[i][j]); 55 } 56 } 57 for(int i = 1; i <= cntx; i++) 58 { 59 for(int j = 1; j <= cnty; j++) 60 slack[j] = INF; 61 while(1) 62 { 63 minz = 1.0 * INF; 64 memset(visx, 0, sizeof(visx)); 65 memset(visy, 0, sizeof(visy)); 66 if(dfs(i))break; 67 double d = INF; 68 for(int i = 1; i <= cnty; i++) 69 if(!visy[i] && d > slack[i]) 70 d = slack[i]; 71 for(int j = 1; j <= cntx; j++) 72 if(visx[j])wx[j] -= d; 73 for(int j = 1; j <= cnty; j++) 74 if(visy[j])wy[j] += d; 75 else slack[j] -= d; 76 } 77 } 78 for(int i = 1; i <= cntx; i++) 79 printf("%d ", cx[i]); 80 } 81 struct node 82 { 83 double x, y; 84 }a[maxn], b[maxn]; 85 double dis(node a, node b) 86 { 87 return -sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)); 88 } 89 int main() 90 { 91 int n; 92 scanf("%d", &n); 93 cntx = cnty = n; 94 for(int i = 1; i <= n; i++)scanf("%lf%lf", &a[i].x, &a[i].y); 95 for(int i = 1; i <= n; i++)scanf("%lf%lf", &b[i].x, &b[i].y); 96 for(int i = 1; i <= n; i++) 97 { 98 for(int j = 1; j <= n; j++) 99 Map[i][j] = dis(a[i], b[j]); 100 } 101 KM(); 102 }