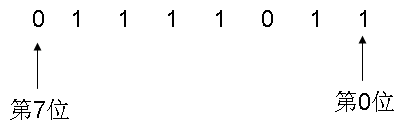我们通常习惯的“十进制”:逢十进一。例如:
但是,在电脑中,“十进制”是不吃香的。换句话说,由于为了使电脑的物理构造更加简单可靠,电脑被设计成“只了解二进制”的工作模式。
二进制
所谓“二进制”,简而言之:逢二进一。
例如,上例的算式,在电脑中就被表示为如下形式:
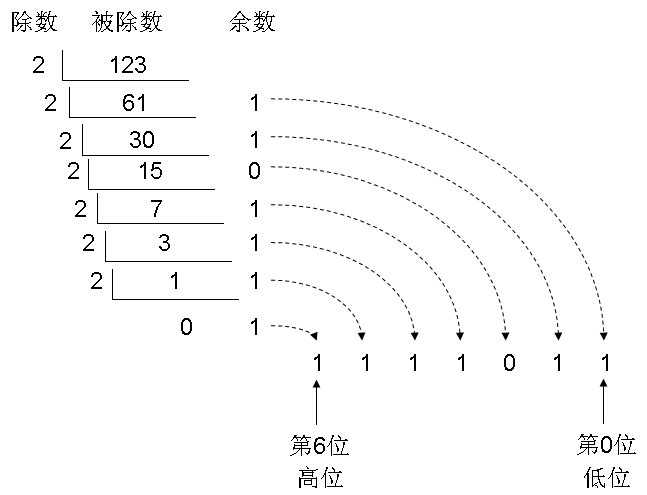
123,被表示为二进制,其(整除)计算过程如下所示:
考虑到一个字节是8个二进制位,所以我们在“最高位”也就是“第7位”上补0,形成如下最终答案:
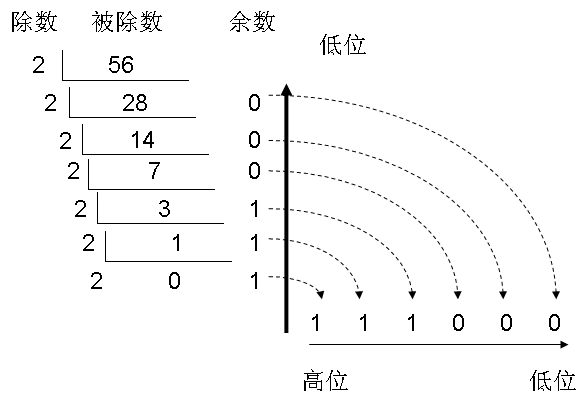
同理,56的转换如下:
56的二进制表示如下:
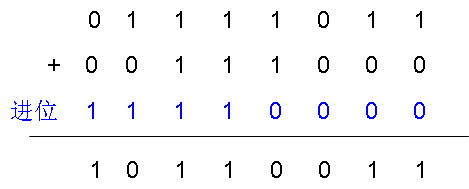
再看加法的过程,注意:逢二进一!
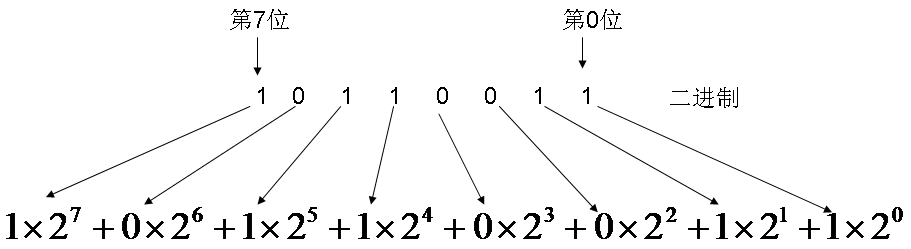
那么,二进制的10110011表示为十进制,应该是多少呢?计算过程如下:
上述这个式子被称为“按权展开式”;按权展开式所得到的结果,一定是10进制的值。
自己算算看,答案是多少?
根据按权展开式,我们总是可以得到“任何进制数所对应的十进制值”。
八进制和十六进制
无论是八进制或是十六进制,都不是电脑所能“理解”的。那为什么需要这两种进制呢?原因是,八进制和十六进制能够有效地提高二进制计算的效率。
换句话说,八进制或十六进制能够很方便地和二进制进行相互转换。
先来说说八进制:
八进制“逢8进一”。注意到:3个二进制位正好能表达1个八进制位的信息。1个八进制位有
共8种状态,对应的3个二进制位是
所以,八进制和二进制的转换方式是十分简单的:3个二进制位转换成对应的1个八进制位。
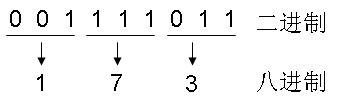
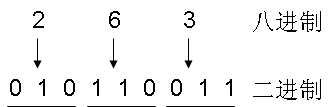
举例来说,二进制到八进制的转换如下图所示:
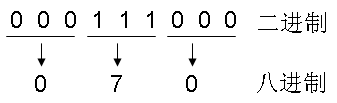
其中,每3位二进制数转换为1位八进制数。注意到上图二进制数中,最左侧的0是我们手动补上去的,为的是凑足3个数进行转换。同理,我们有下图:
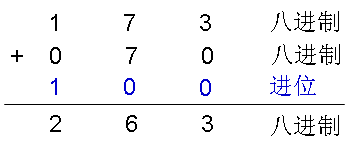
把上述转换得到的2个八进制数相加;
按权展开,验算一下:
这与十进制数计算的答案是相符的。说明我们的八进制运算是正确的。
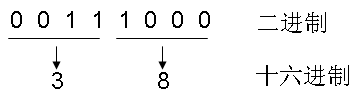
最后,我们也可以把八进制转为二进制,得到二进制的答案:
(和先前的二进制形式的计算结果是相符的)
由上运算过程可见,八进制的表示法,比二进制的表示法来得方便。(尽管电脑不认识八进制,但是可以提高我们手工计算的速度。)
再来看看十六进制:
这和八进制的形式很相似。只不过:
十六进制“逢16进一”。1个十六进制位对应的数值表示是:0~9,A,B,C,D,E,F;其中,A,B,C,D,E,F分别对应十进制的10,11,12,13,14,15。我们注意到:4个二进制位正好能表达1个十六进制位的信息。1个十六进制位有
共16种状态,对应的4个二进制位是
所以,十六进制和二进制的转换方式是十分简单的:4个二进制位转换成对应的1个十六进制位。
以上题为例,我们再用十六进制做个转换计算的例子:
另一个数:
二者相加:
按权展开,得到:
![]()
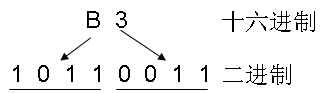
同样地,我们也可以很方便地把上述十六进制的值再转为二进制的表达形式:(1位十六进制扩展为4位二进制)
由上运算过程可见,十六进制的表示法,比二进制的表示法来得方便。(尽管电脑也不认识十六进制,但是它却可以提高我们手工计算的速度。)
至此,我们完整地讨论了二进制、八进制、十进制、十六进制之间的转换问题。在具体的计算和转换过程中,需要灵活掌握和运用。
特别地,由于时间关系,本文只讨论了加法的问题。至于减法,读者可以根据文中所述的原理,自己推算一下。
谢谢观赏!
![clip_image002[11] clip_image002[11]](https://images.cnblogs.com/cnblogs_com/fzd19zx/201102/201102181237306239.gif)