一个包含重复元素的升序数组在经过旋转之后,可以得到下面可视化的折线图:
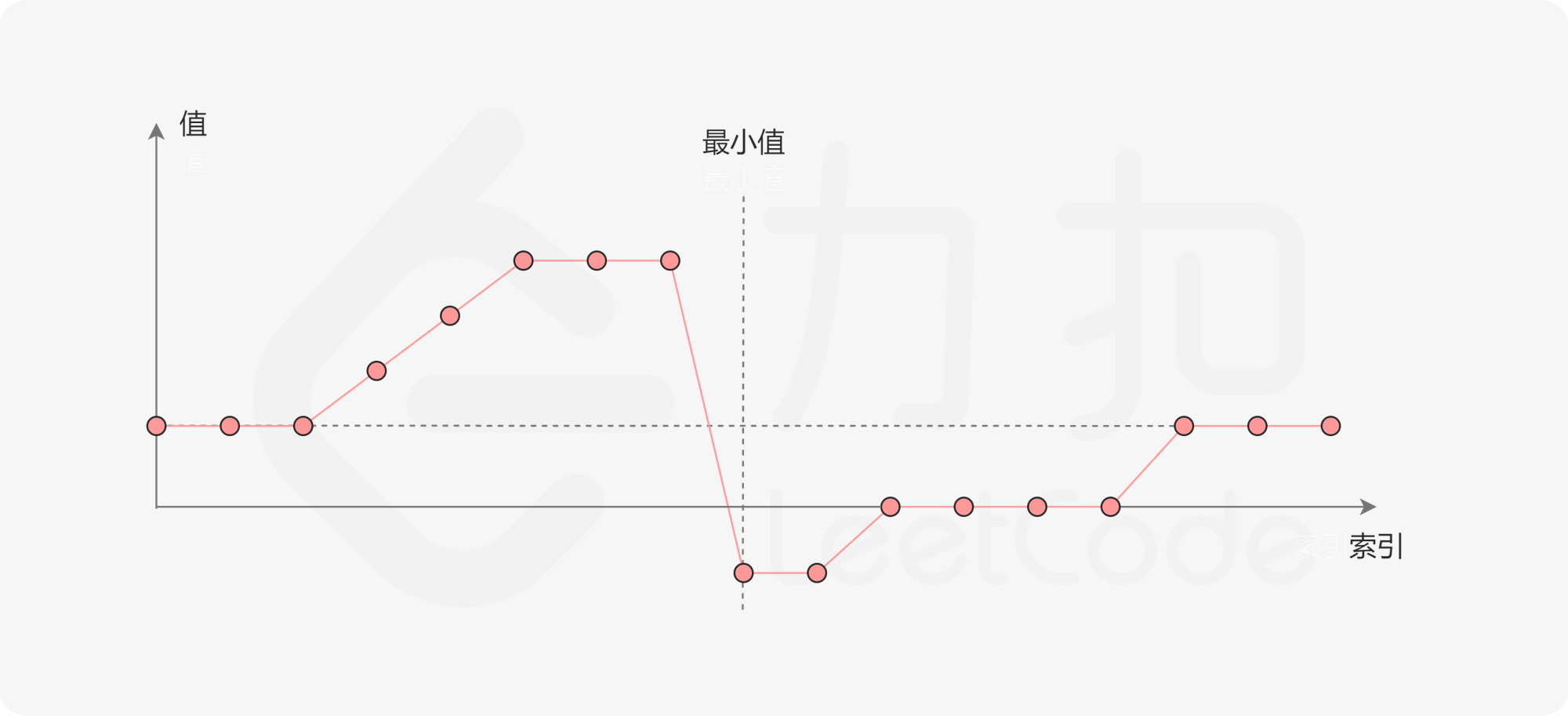
其中横轴表示数组元素的下标,纵轴表示数组元素的值。图中标出了最小值的位置,是我们需要查找的目标。
我们考虑数组中的最后一个元素 x:在最小值右侧的元素,它们的值一定都小于等于 x;而在最小值左侧的元素,它们的值一定都大于等于 x。因此,我们可以根据这一条性质,通过二分查找的方法找出最小值。
在二分查找的每一步中,左边界为 low,右边界为 high,区间的中点为 pivot,最小值就在该区间内。我们将中轴元素 numbers[pivot] 与右边界元素 numbers[high] 进行比较,可能会有以下的三种情况:
第一种情况是 numbers[pivot]<numbers[high]。如下图所示,这说明 numbers[pivot] 是最小值右侧的元素,因此我们可以忽略二分查找区间的右半部分。
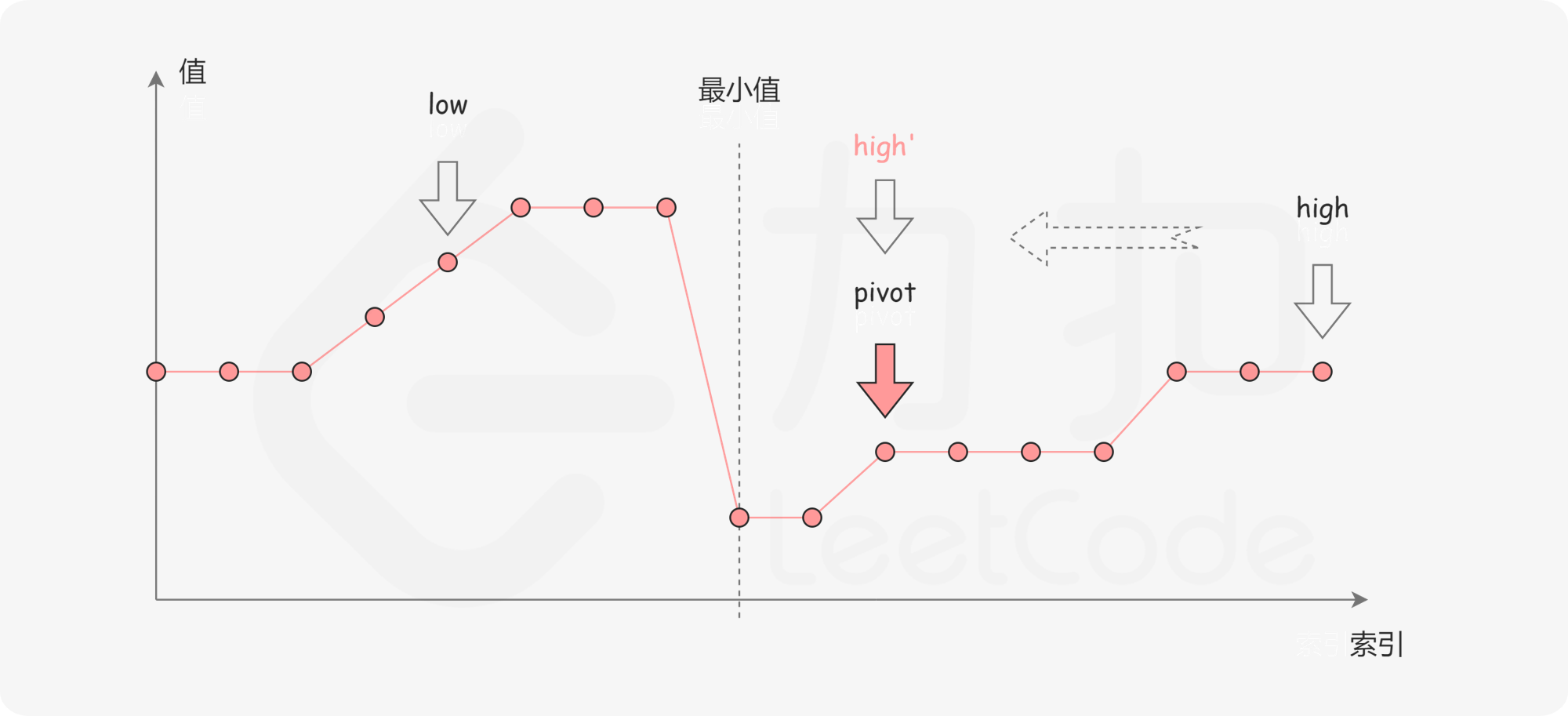
第二种情况是 numbers[pivot]>numbers[high]。如下图所示,这说明 numbers[pivot] 是最小值左侧的元素,因此我们可以忽略二分查找区间的左半部分。
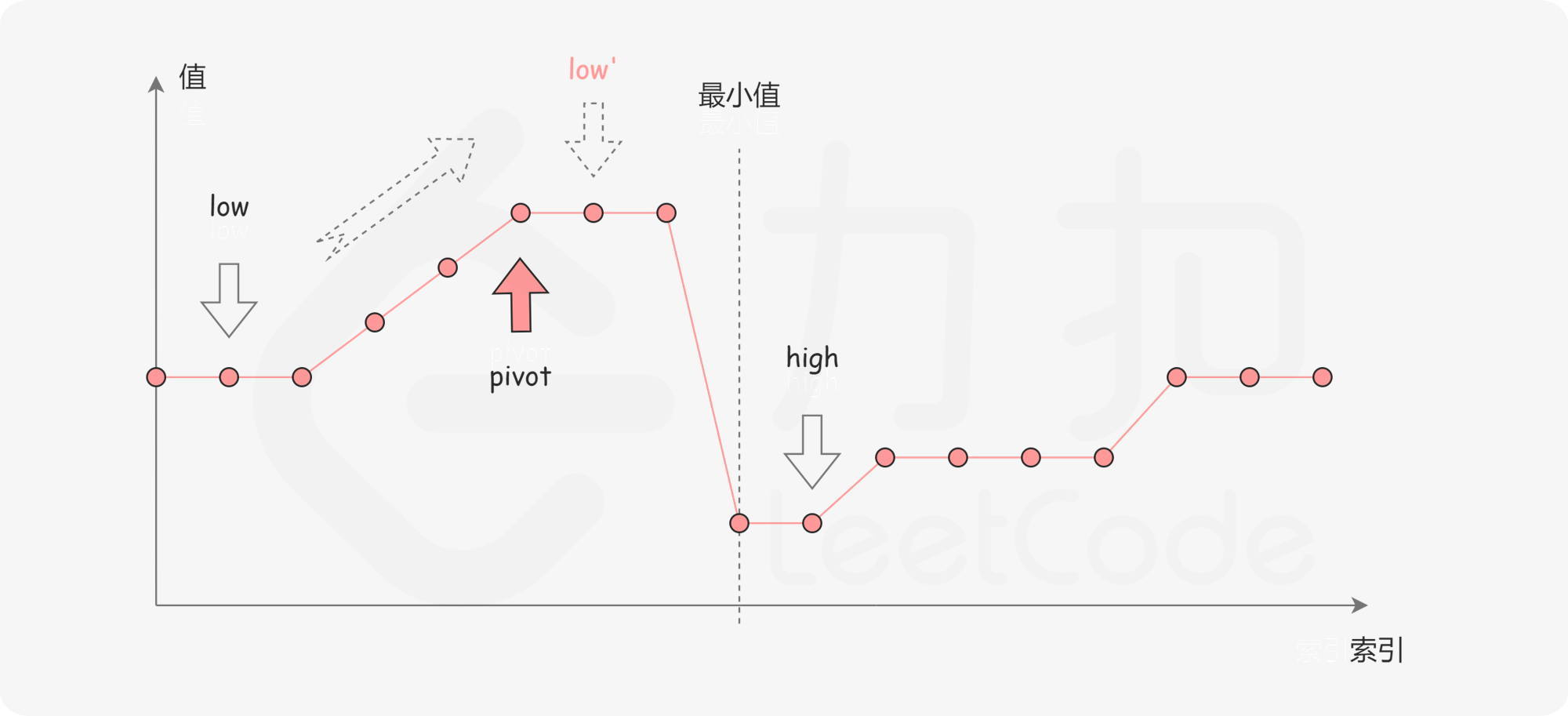
第三种情况是 numbers[pivot]==numbers[high]。如下图所示,由于重复元素的存在,我们并不能确定 numbers[pivot] 究竟在最小值的左侧还是右侧,因此我们不能莽撞地忽略某一部分的元素。我们唯一可以知道的是,由于它们的值相同,所以无论 numbers[high] 是不是最小值,都有一个它的「替代品」numbers[pivot],因此我们可以忽略二分查找区间的右端点。
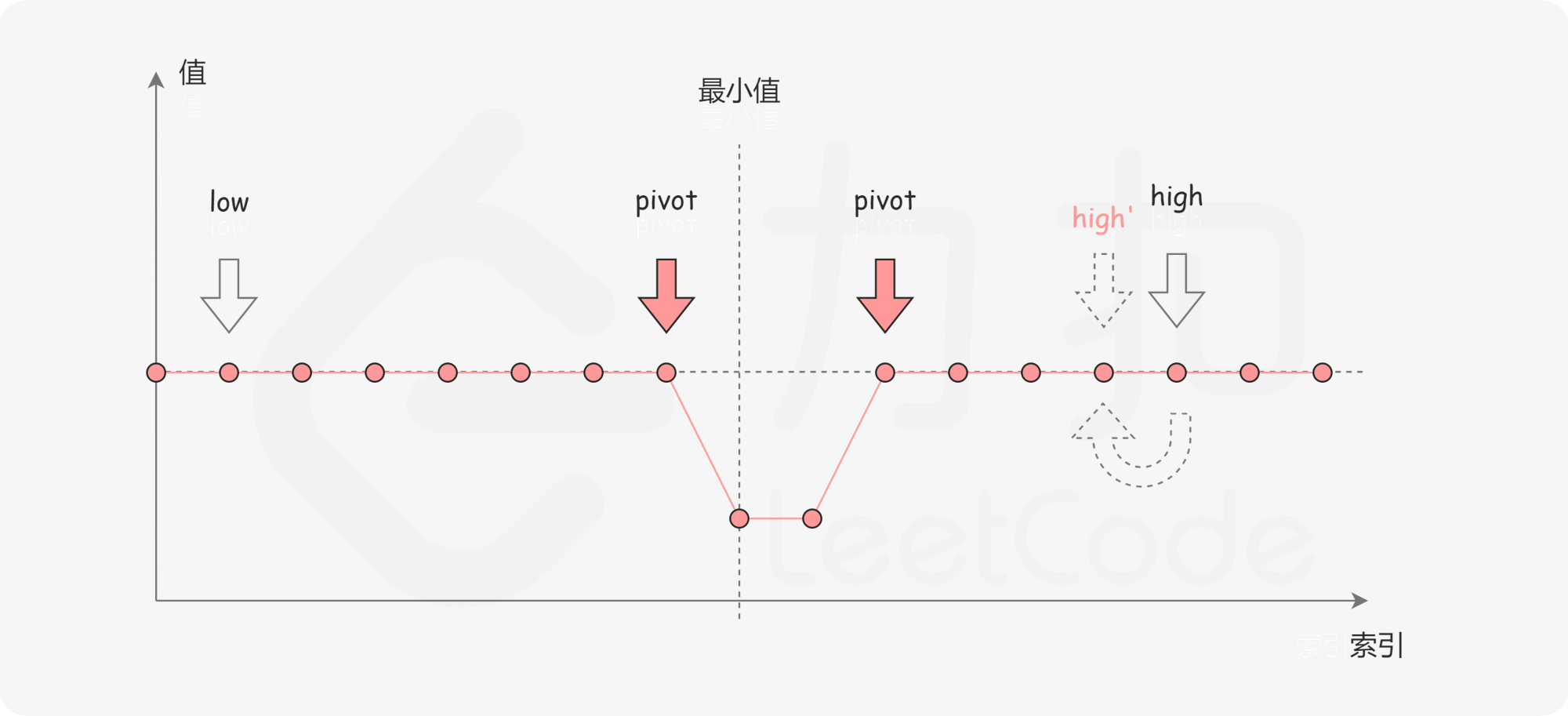
当二分查找结束时,我们就得到了最小值所在的位置。
class Solution {
public:
int minArray(vector<int>& numbers) {
int n =numbers.size();
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if(numbers[mid] < numbers[r])
r = mid;
else if(numbers[mid] > numbers[r])
l = mid + 1;
else
r--;
}
return numbers[l];
}
};