12.食物链 并查集

 

 

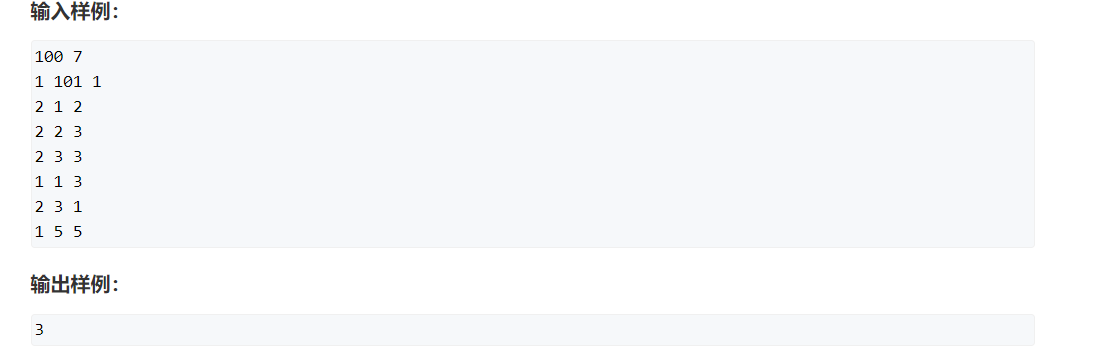
 这是用并查集维护每个点和根节点的关系

只要我们知道了每个点和根节点的关系，就可以知道每两个点之间的关系

就和族谱一个道理，简单举个例子

假设族谱里最上面的那个人（根节点）是爷爷

然后A是爷爷（根节点）的儿子

B是爷爷（根节点）的孙子

那么就可以知道A和B的关系，A和B是父子

大致就是这个意思

然后这一题如何确定每个点和根节点的关系呢

由于是三种动物循环被吃

那么就用每个点到根节点的距离，来表示它和根节点的关系

我们说的这个距离，是这个点到根节点的真正的距离mod 3后的值，mod 3之后只会有3个值，0和1和2

如果某个点到根节点的距离mod 3是1的话，表示这个点可以吃根节点

如果某个点到根节点的距离mod 3是2的话，表示这个点可以被根节点吃

如果某个点到根节点的距离mod 3是0的话，表示这个点和根节点是同类

总结下来就是

mod 3 余 1的点，就是所有可以吃根节点的点、

mod 3 余 2的点，就是所有可以被根节点吃的点，也是所有可以吃mod 3 余 1的点

mod 3 余 0的点，就是所有和根节点同类的点，也是所有可以吃mod 3 余 2的点

根节点可以看成到自己的距离是0，所以就有

余0的吃余2，余2的吃余1，余1的吃余0

所以就可以把本题中的所有集合归为上面三大类

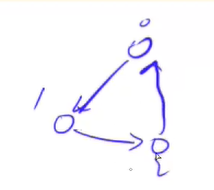
 如果说x吃y，y就是0，x就是1

吃1的就是2，z吃x，z就是2

吃2的就是3，3 mod 3 = 0，也就是0

k吃z，那k就是0

 总结下来就是用并查集维护每个点到根节点的距离

但是我们实际记录的是每个点到它的父节点的距离

 在做路径压缩时，再进行更新

#include <bits/stdc++.h>
using namespace std;
const int N = 50010;
int p[N], d[N];
//p存储父节点，d是距离
int find(int x) {
    if (p[x] != x) { //如果x不是树根的话
        int t = find(p[x]); //t存储了根节点是谁
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        p[i] = i; //初始化，每个点是一个集合，每个点到自己的距离d是0
    }
    int res = 0; //假话个数
    while (m--) {
        int t, x, y;
        cin >> t >> x >> y;
        if (x > n || y > n) {
            res++;
        } else {
            int px = find(x), py = find(y);
            if (t == 1) { //如果说x和y是同类
                if (px == py && (d[x] - d[y]) % 3 != 0) { //如果他们俩已经在一个树上了，用关系推理
                    res++; 
                } else if (px != py) { //说明没在一个树上
                    p[px] = py;
                    d[px] = d[y] - d[x]; //见注解一
                }
            } else {
                if (px == py && (d[x] - d[y] - 1) % 3 != 0) { //x吃y，x比y大一
                    res++;
                } else if (px != py) {
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }
    cout << res << endl;
    return 0;
}

注解一：

 

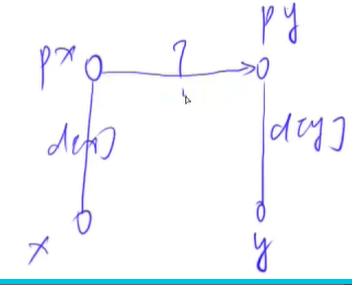
 当我们把？这个数填好之后，x和y是同类

那么在mod 3的意义下，d[x] + ? = d[y]