2.完全背包问题

 完全背包问题是每件物品有无限个

完全背包问题的状态表示和01背包问题一样

dp[i][j]表示只看前i个物品，总体积<= j的最大价值

状态计算：

　　按照第i个物品选了多少个来分

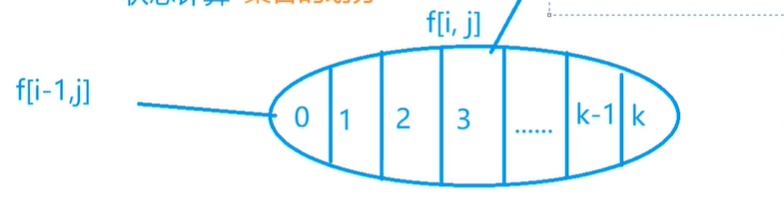
 然后综合起来就是

k是枚举的第i个物品的个数，k = 0， 1， 2，...

三层循环的二维做法

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dp[N][N];
int v[N], w[N];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> v[i] >> w[i];
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= m; j++) {
            for (int k = 0; k * v[i] <= j; k++) { //枚举一下物品个数，k个物品一定要小于等于j 
                dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i] * k] + w[i] * k);
            }
        }
    }
    cout << dp[n][m] << endl;
    return 0;
}

完全背包问题可以优化乘两层循环

 这是两层循环，二维的解法

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dp[N][N];
int v[N], w[N];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> v[i] >> w[i];
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= m; j++) {
            dp[i][j] = dp[i - 1][j];
            if (j >= v[i]) {
                dp[i][j] = max(dp[i][j], dp[i][j - v[i]] + w[i]);
            }
        }
    }
    cout << dp[n][m] << endl;
    return 0;
}

完全背包问题也可以优化到一维

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dp[N];
int v[N], w[N];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> v[i] >> w[i];
    }
    for (int i = 1; i <= n; i++) {
        for (int j = v[i]; j <= m; j++) {
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    cout << dp[m] << endl;
    return 0;
}