蓝桥杯 排列问题

问题描述

　　求一个0～N-1的排列（即每个数只能出现一次），给出限制条件（一张N*N的表，第i行第j列的1或0，表示为j-1这个数不能出现在i-1这个数后面，并保证第i行第i列为0），将这个排列看成一个自然数，求从小到大排序第K个排列。

数据规模和约定

　　N<=10，K<=500000

输入格式

　　第一行为N和K,接下来的N行，每行N个数，0表示不能，1表示能

输出格式

　　所求的排列

样例输入

3 2
0 1 1
1 0 0
0 1 0

样例输出

1 0 2
解释：
对于N=3的没有任何限制的情况
第一：0 1 2
第二：0 2 1
第三：1 0 2
第四：1 2 0
第五：2 0 1
第六：2 1 0
根据题目所给的限制条件由于2不能出现在1后面，0不能出现在2后面
第一：0 2 1
第二：1 0 2
第三：2 1 0
参考自https://blog.csdn.net/weixin_44778155/article/details/104672498
这道题目题意比较难理解，简单解释一下。
首先我们生成一个0~n-1的全排列，比如n=3的时候，全排列按顺序为：

第一：0 1 2
第二：0 2 1
第三：1 0 2
第四：1 2 0
第五：2 0 1
第六：2 1 0
然后我们给出了限制，这个限制是通过一个n*n的矩阵给出的，我们开一个二维数组vis[][]记录这个矩阵。
在这个矩阵里，从左上往右下i=j这条对角线上的0没有用，我们不用看。
我们只看其他位置有没有0，在样例里也就是vis[1][2]=0，vis[2][0]=0

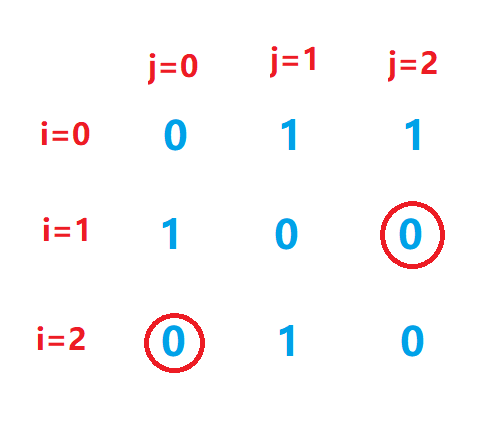
就是说2不能紧贴着跟在1的后面，中间隔了几个数然后2在1后面是可以的。所以上面六个全排列中的第一，第四不符合要求，删去。
然后0不能紧贴着跟在2后面。上面的第五删去。
所以剩下的全排列是：

第一：0 2 1
第二：1 0 2
第三：2 1 0
然后样例k=2，所以输出第二个全排列1 0 2
然后这段代码就好理解了。

#include <bits/stdc++.h>
using namespace std;
int n, k, cnt;
int a[20];
int vis[20][20];
bool check() { //check函数用于判断当前这个全排列是否符合题意 
    for (int i = 1; i < n; i++) { //遍历这个全排列，看看是否存在某个数不能紧贴在某个数后面的情况 
        if (vis[a[i - 1]][a[i]] == 0) {
            return false;
        }
    }
    return true;
}
int main() { 
    cin >> n >> k;
    for (int i = 0; i < n; i++) {
        a[i] = i; //生成0~n-1的序列 
    }
    for (int i = 0; i < n; i++) { //输入限制 
        for (int j = 0; j < n; j++) {
            cin >> vis[i][j];
        }
    } 
    do {
        if (check()) { //判断这个序列是否符合要求 
            if (++cnt == k) { //若符合要求，++cnt。求到第k个符合条件的全排列的话，break 
                break;
            }
        } 
    } while (next_permutation(a, a + n));
    for (int i = 0; i < n; i++) { //输出这个全排列 
        cout << a[i] << " ";
    }
    cout << endl;
    return 0;
}